作って理解する浮動小数点数① 基本編
以前も浮動小数点数の記事を書いた(作る側の気持ちで理解する浮動小数点数 - in neuro)。だがその時は、浮動小数点数に関するアイデアの説明しかしておらず、実際の「浮動小数点数(IEEE754)」については説明しなかった。今回の記事の目的は、実際の浮動小数点数についてちゃんと解説し、またいくつかの演算をビット単位で自力で書くことで、理解を深めることである。
現実の浮動小数点数
演算について書くとは言ったが、その前に少し浮動小数点数についての基本的なアイデアをおさらいしておこう。このあたりの知識は演算を理解する際にも必要になる。すでに知っている人には退屈だろうから、演算編で引っかかったときだけ見るのでも構わない。
浮動小数点数の基本的構造
浮動小数点数はその名の通り、小数点の位置が動的に変わる数である。基本的な表現方法は1.234x10-5のような指数表記と同様だ。
例えば単精度(32bit)浮動小数点数のフォーマットは、以下のようになっている。1.234x10-5のバイナリ表現を見てみよう。
|0|0110'1110|100'1111'0000'0111'1110'0101| | '-+-----' '-+------------------------' | | +-> 23-bit mantissa(仮数部) | +-> 8-bit exponent(指数部) +-> sign bit(符号)
一番最初のビットは符号ビットであり、これが0だと正の数、1だと負の数である。よってこれ以降の部分は、表す数の絶対値を決めている。
続いて8bitの指数部がある。ここでは2-17を表している。これは符号なし整数なのだが、負の値を表現するためにバイアスという値を使う。単精度浮動小数点数の場合はバイアスは-127であり、この8bitを符号なし整数として解釈したものから127を引いた値が指数として扱われる。なので、今回は0b01101110 = 110 (decimal)から、指数は-17となる。
さらに、指数部には特別な値があり、最大(0b1111'1111)と最小(0b0000'0000)の場合には特殊な値を表す。詳しくは、のちの「非正規化数」と「非数と無限」を参照されたい。
残りの23bitは仮数部である。ここでは1.1001111...の部分を表している。2進数なので、0.1は1/2であり、0.01は1/4だ。仮数部の最初のビットは1の位ではなく1/2の位で、続くビットは1/4の位, 1/8の位, 以下同様となる。では仮数部は0.xxxとして[0, 1)の範囲を表現しているのかというとそうではなく、仮数部は1.xxxのxxxの部分を表現している。つまり、1の位に暗黙の1が存在しており、実際に表現している範囲は[1, 2)ということになる。
1の位より上の位を持たず、1の位が非ゼロになるように指数を調整した指数表記を正規化数と呼ぶ。そして浮動小数点数は基本的に正規化されている。例えば1.0110x23は正規化されているが、0.1011x24は正規化されていない。2進数では非ゼロな数というのは必ず1になるので、常に非ゼロである1の位は効率化のため符号化の際に省略されている。これはケチ表現と呼ばれる。
なぜ1から2の範囲なのか
さて、ではなぜ0.xxxではなく1.xxxなのかについて少し考えてみよう1。そういう風に決まっているとして終わらせてしまうこともできるのかもしれないが、納得は得られない。これは以前の記事でも書いたが、コンパクトに書き直しておく。
まず、前提として我々は二進数を用いており、また指数部と仮数部を分割したというところまでは認めてしまおう。その上で、我々の目標はできるだけ効率よく広い範囲の実数を高精度に符号化することである、ということも同意してもらいたい。この条件で、仮数部が表現する範囲の良さを考えよう。
まず、0.XXXの場合を考えてみる。この場合、仮数部が表現する範囲は最小で0.0000...、最大で0.1111...なので、[0, 1)になる。これに指数を追加することを考えよう。指数が追加されたことにより、全体を例えば2倍した範囲を表現できるようになる。そのような範囲は何から何までになるだろうか? 0.000...0x2から始まり、0.111...1x2までの範囲になるだろう。これは、[0, 2)の範囲ということになる。振り返ってみると、我々はすでに[0, 1)の範囲は指数が0の場合にすでに精度よく表現できている。この上分解能を1ビット落とした表現で[0, 2)の範囲の一部分として[0, 1)の範囲を表現しなおすことにメリットはない。指数が-1の場合も同じで、[0, 1/2)の範囲が[0, 1)の範囲と被ってしまう。被ってしまうということは同じ値の表現方法が複数あるということで、符号化の効率もよくないし、実装上も不都合が多い。
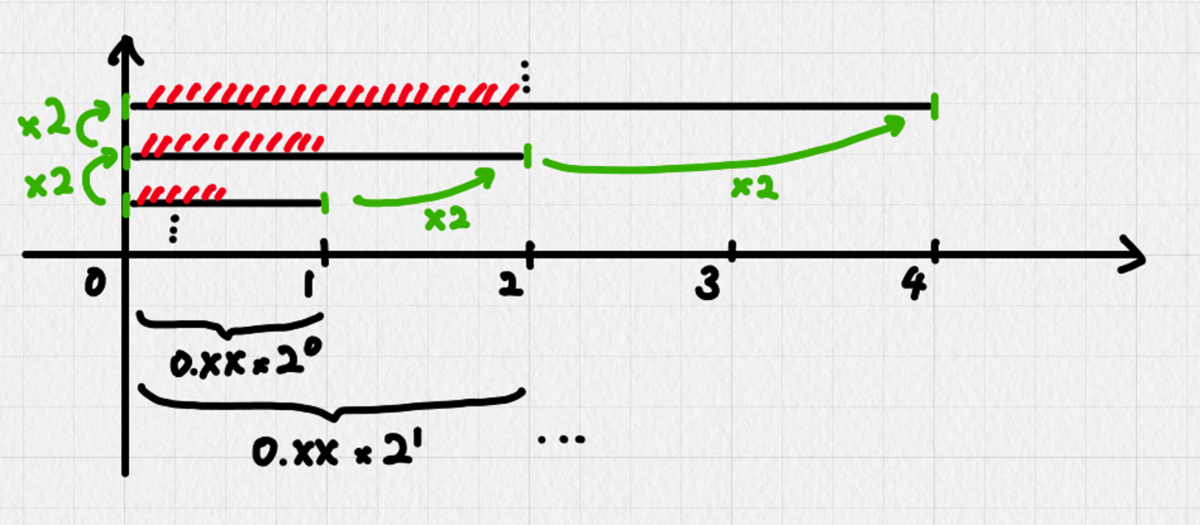
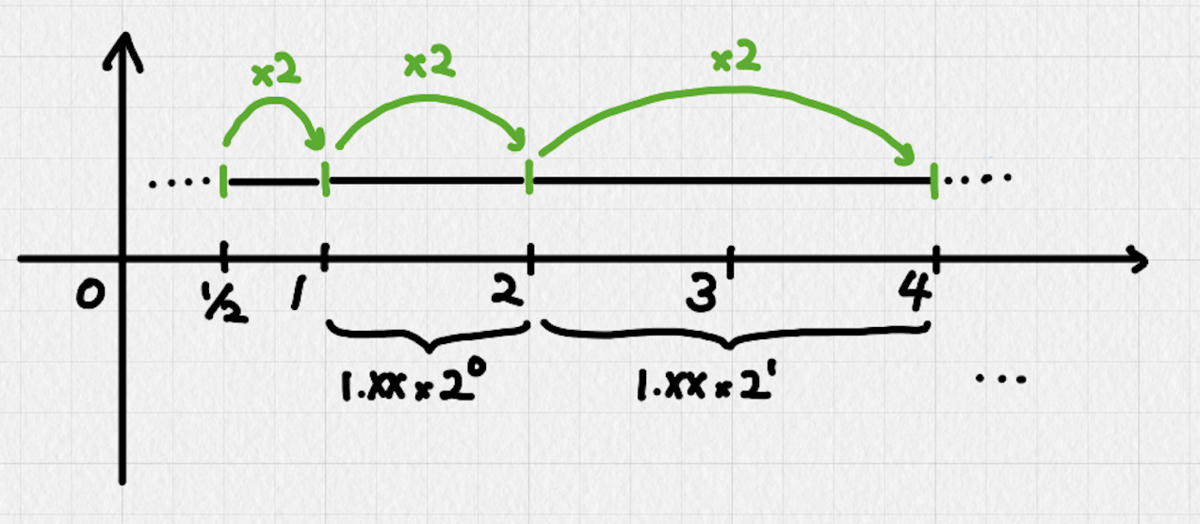
対して、1.XXXの場合を考えよう。この場合、仮数部が表現する範囲は最小で1.000...0、最大で1.111...1なので、[1, 2)になる。指数が1だった場合は、範囲は[2, 4)になり、指数が0のときの[1, 2)と被らないどころか綺麗に繋がる。逆の場合も同様で、指数が-1なら[1/2, 1)になるため、こちらも綺麗に繋がる。このようにして、被りが生じないまま数直線上の大部分が表現できることになる。
この性質は、範囲を[a, b)とし、基数をrとした場合、a * r = bが成立していればどのような組み合わせでも生じる。もし電子回路が-1, 0, 1の3状態で動いていたなら、基数は3になり、範囲は[1, 3)になっていただろう。……いや、ビットが3状態でそれぞれ {-1, 0, 1} の場合は符号ビットが存在しないから(ビット単位で正負があるので)、素直に(-1, 1)の範囲だろうか? いやそれだと範囲が被ってしまう。仮数部にバイアスをつけて2±1にすればいいのだろうか。これなら3倍して6±3にすると綺麗に繋がるが、範囲内に負の値を含まないようにしたので符号ビットが必要になり、符号ビットがゼロの場合が無駄になってしまう。無駄にしないようにするには、符号ビットがゼロの場合にゼロと非数・無限大を詰め込めばいいだろうか。そういう研究もありそうではある。
ゼロ
個人的にはゼロはビットレベルでも00000000であった方が簡単そうな気がする。そして実際に、浮動小数点数のゼロは00000000である。正確には、指数部と仮数部が両方ゼロである場合、値はゼロとなる。しかし、浮動小数点数が符号ビットを持っている都合上ゼロにも符号があり、+0と-0が存在している。演算の際に特に違いはない。
これは先に述べた「指数部が0b0000'0000の際の特殊な値」のうちの一つである。感覚的にも、指数が小さくなるとゼロに近づいていくわけで、指数部が最小の値になると突然ゼロになるというのも、そこまでの飛躍には感じないのではなかろうか。
非正規化数
さて、ゼロが「指数部と仮数部が両方ゼロである場合」なら、指数部がゼロで仮数部が非ゼロだった場合はどんな値になるのか。それが非正規化数である。これは先に述べた「指数部が0b0000'0000の際の特殊な値」のもう一つのパターンとなる。
非正規化数の指数部はゼロであるため、絶対値が小さい側にあるのだろうと予想できる。そして実際に非正規化数は絶対値が小さい。これがどこに位置しているかというと、最小の正規化数からゼロまでの間である。最小の正規化数は単精度浮動小数点数においては1.000x2-126である。指数部がゼロでない最小の値、つまり1のとき、バイアスを考慮するとその指数は-126になるためだ。非正規化数を考慮しなければ、この数の次に絶対値が小さい値は0になる。0 ~ 1 x2-126の範囲は表現されない。同じくらい細かい、1 ~ 2 x2-126の範囲は23bitもの精度で表現されるにもかかわらず。
この範囲を正規化数で埋めようとしても、右半分([2^(-127), 2^(-126)))しか埋まらないのは簡単にわかる。そこで、この範囲を1~2 x2-126と同じ幅で分割してしまうというのが非正規化数である。その表現範囲は[0, 1x2-126)となる。よって非正規化数の1の位はゼロとなり、その名の通り正規化されていない数となる。正規化数とは、最初の意味のある桁が1の位であり、かつ1の位が非ゼロなものを指すのであった。なので非正規化数ではケチ表現での暗黙の1は存在せず、1桁目には暗黙の0が存在する。

f32なら2-126)で表現する。全てを正規化数とした場合(上段)、赤色斜線の範囲[0, 2^(-127))が表現できない。
ところで、この表現での最小の数は0であり、その表現は0.0000x2-126なので、指数部と仮数部がともにゼロとなる。これは先に述べたゼロの表現と一致している。このようにすることで、最後の正規化数からゼロまでが綺麗に繋がる。
非数と無限
浮動小数点数演算の結果として、浮動小数点数の範囲内では表現できないような値が出現することがあり得る。そのような数を表現するために、浮動小数点数には非数(NaN)と無限大(Inf)が存在する。これらが、「指数部が0b1111'1111の際の特殊な値」である。NaNは置いておくとして、無限大を導入することを認めてそれをどう符号化するかを考えれば、指数部が大きくなると値は指数的に大きくなるわけで、指数が最大値になると無限大になるというのがちょうどいい場所だろう。
NaNとInfは、指数部のビットがすべて1、つまり指数部が最大の値を取る。そのうえで、仮数部がゼロであればInf、そうでなければ(一つでも1であるビットがあれば)NaNとなる。よってNaNは仮数部だけで223-1(倍精度なら252-1)通りの異なる値を取ることができる。余談だが、言語処理系などの実装では、この隙間に小さな整数を埋め込むというテクニックが存在する(NaN boxing)2。また、符号ビットに関しては制約がないので、InfとNaNにも正負がある。NaNはともかくとして、Infの正負には演算においても意味がある。
これらは特定の演算の結果として出てくる。例えば、演算の結果が浮動小数点数の範囲では表現しきれない大きな値になったときは、通常はInfが帰ってくることになる。非数は、0/0 や inf - inf 、そして複素数への変換が暗黙に行われない場合のsqrt(-1)などの結果として発生する。
InfやNaNなどの特殊な数は、演算においても特別扱いされるため、実装する際には念頭に置いておく必要がある。これらは演算を実装する際に必要に応じて説明する。
丸め
浮動小数点数の桁数が有限である以上、計算結果がその範囲を超えた際には、下の桁を忘れざるを得ない。そのような場合に下の桁をどう扱うかが、丸めモードで規定されている。
通常は「最近接(偶数)丸め」が採用されており、今回の記事もこれだけを考慮する。最も使われており、かつ最もややこしい丸めモードであるように思う。これは基本的には最近接の値に丸めるという方針だが、ちょうど真ん中(二進数なので0.101は0.10と0.11のちょうど真ん中にある)の場合には、上の桁が偶数になるように丸めるというモードだ(先の例の場合、0.10にする)。この丸めモードでは、切り上げるか切り下げるかを決定するのに、「今から落とすので丸めたい桁」「丸めたい桁より下がすべてゼロかどうか(丸めたい桁は前後の数のちょうど真ん中かどうか)」「丸めたい桁の一つ上の桁は偶数かどうか」の全てを知っていなければならない。
ほかのモードには、最近接(0から離れる)丸め、切り上げ、切り下げ、切り捨てなどがある。が、今回は深入りしない。基本的には、上記の情報に加えて符号ビットを知っていれば問題なく実装できるはずだ。
おわりに
浮動小数点数の性質についてのおさらいはもうこれで十分だろう。これだけわかっていれば今後演算を考える際に困ることはない。次回は実際に浮動小数点数の加算を考えてみる。
より細かくIEEE仕様について知りたい人には、技術書典で販売されていた『浮動小数点数小話』(だめぽラボ)が日本語かつよくまとまっており、参考になる。
-
一応注意しておくと、この記事の内容は特に浮動小数点数の策定の歴史などについて調べたものではなく、私が勝手に解釈したものなので、この形が選ばれた実際の理由とは異なる可能性がある。↩
-
例として、動的型付け言語の処理系を書いているとしよう。変数を保持する型は基本的にはオブジェクトへのポインタにしておけばよいのだが、浮動小数点数や32bit整数くらいの小さなプリミティブ型ならポインタを経由させずそのまま持っていた方が効率が良い(しかも、プログラム内で出てくる大抵の整数は32bitの範囲よりも十分小さく、余裕をもって格納できる)。というわけで、変数の内部表現を浮動小数点数にしておいて、NaNの場合は浮動小数点数以外の値である、ということにする。そしてNaNの使われていない仮数部を32bit整数やシンボルID、オブジェクトへのポインタを格納するために使うということだ。いや32bit整数が64bit浮動小数点数の仮数部(52bit)に入るのはわかるが、ポインタは無理だろう? と思われるかもしれないが、実際にはx86_64ではアドレスは実質的には48bitしか使われておらず(『低レベルプログラミング』などを参照)、ギリギリ入るのである。↩