2023-12-16

2023年のコンパイル時レイトレーシング

C++

これは

の12/16の記事です。やばいもう16日が終わってしまう！

はじめに

太古の昔、あるC++プログラマ *1がtemplateの再帰と特殊化を使ってコンパイル時に計算ができることを「発見」*2 *3したその日から、C++とコンパイル時計算は分かちがたく結びついています。

言語機能を本来意図されていなかった方法で活用する曲芸的な技巧だったコンパイル時計算は、その強力さを買われコミュニティを席巻し、C++11での constexpr の導入によりある意味で公式に認められたものとなりました。導入当初は return 文一つだけしか持てなかった constexpr 関数は、それでも三項演算子による条件分岐や再帰によってコンパイル時計算を大いに盛り上げました。そしてC++14で条件分岐、ループ、変数の書き換えが、C++17ではラムダが、C++20では仮想関数と動的メモリ確保が、とコンパイル時計算で利用できる言語機能は増え続けており、今では通常のプログラミング言語と遜色ないと言えるところまで来ています。

本記事では、まず constexpr の制限緩和の歴史を追いかけ、結果C++23でコンパイル時計算がどれほど簡単になったのかを、レイトレーシングを題材に見ていきます。レイトレーシングはC++のコンパイル時計算では伝統ある（？）題材で、ボレロ村上さんの代表作の一つと言えるでしょう。彼は芸術家にして日本で指折りのC++プログラマであり、またC++コミュニティ全体に絶大な影響を与えた constexpr 世界の開拓者でもありました。レイトレーシングは、コンパイル時計算でどれほどのことができるのかを示す実例として、重い処理であることが想像でき、かつ視覚的インパクトを伴う形でその可能性を見せつける、いい題材だと思います。

今回はGitHubに実際に書いたものを上げてありますので、気になる方はそちらもご覧ください。とはいえ、C++23が強力すぎて、ほとんど普通のコードになっていますが……。

はじめに
constexprの発展史
C++23でのコンパイル時レイトレーシング
おわりに

constexprの発展史

最初はコンパイル時レイトレーシングのコードの解説だけで書こうと思ったのですが、書いてみたらあまりにも普通のコードになってしまったため、追加で constexpr の発展を時系列で見ることにしました。

ただ、見通しが甘すぎて長大になったので（甘すぎる）結構端折っています。個別の要素に関してはもっとしっかりとした解説記事が別にあることが多いので、より詳細に知りたいという型は調べてみてください。

C++11

`constexpr`変数

constexprな変数は、コンパイル時に値が計算され確定し、実行時にそれを書き換えることはできなくなります。これらの値はコンパイルの結果として即値としてエンコードされたり、.rodataセクションに置かれたりするでしょう。 constexpr指定できる変数はリテラル型に限られます。

`constexpr`関数

constexprな関数はコンパイル時に計算できる関数ですが、変数とは違って実行時に使うことも可能です。結果をconstexpr変数にする場合はコンパイル時に実行され、このときは引数もコンパイル時定数である必要があります。

constexpr関数は変数を変更することはできませんでした。よって、計算結果は引数の参照経由などではなく、値として返す必要があります。そのため、voidを返すこともできませんでした。副作用がなく引数の変更もできないなら、voidを返す関数は何もできないからです。

さらに、constexpr関数の本体で許されるのは、型エイリアスやstatic_assertを除けば、return文だけでした。よって、forやwhileなどの繰り返し計算やifによる分岐はできませんでした。繰り返しは再帰呼び出しで、分岐は三項演算子cond ? then : elseで行う必要があります。

また、メンバ関数をconstexprにすると暗黙にconstになってしまいます。 C++11ではconstexpr関数内で変数を書き換えられなかったため、非constなメンバ関数は存在意義がなかったというところでしょうか。この制限はC++14で、constexpr関数内での変数の更新が許可されると同時に緩和されました。

C++14

制限緩和

C++14ではconstexpr関数に大幅な制限緩和が行われました。具体的には、ifやswitchによる分岐、forやwhileによるループ、未初期化変数の宣言と変数の変更が許可され、ほとんど普通の関数になりました。

また、変数を変更できるようになったため、voidを返す関数も許可されました。引数を更新してvoidを返すような関数がconstexprになれるようになったからです。

さらに、変数を変更できるようになったので、constexprなメンバ関数が暗黙にconstになるという制限も取り払われました。constexpr文脈内で呼び出しても、クラスが変更される可能性が出てきたからです。

提案では、C++11の制限されたconstexpr関数で何かを書こうとするとかなりの面倒が生じること、D言語では当時既にこのような機能が存在していることなどが理由として挙げられています。*4 特に、標準ライブラリ関数をconstexpr対応させる際にも面倒が生じることが主張されています。例えば、イテレータのインクリメントは値の変更を（当然ながら）伴うので、constexprにできない、という点が指摘されています。

https://www.open-std.org/jtc1/sc22/wg21/docs/papers/2013/n3597.html

`<array>`, `<chrono>`, `<complex>`, `<initializer_list>`, `<tuple>`, `<utility>`の一部

制限緩和と同時に、複数のライブラリ機能がconstexprに対応しています。

<array>のoperator[]とat()のうち、constなものがconstexprに対応しています。これはC++11時点での提案だからでしょうが、C++14で変数の変更が可能になりconstexprメンバがconstにならなくなったというのに標準ライブラリはまだそれには対応していないというのは、少しやきもきするところではあります。

また、<chrono>の時刻演算がconstexprになっています。内部で使われている<ratio>はtemplate metaprogrammingによって実現されているため、コンパイル時計算との親和性はもとから高かったのかもしれません。

<complex>では、コンストラクタと比較演算子、それからreal(), imag()がconstexprになっています。これも、C++11時点での提案だからでしょうが、real()やimag()のconstなバージョンだけがconstexprになっています。演算などはまだサポートされていないようです。

<initializer_list>と<tuple>と<utility>、特に<utility>はstd::pairに対してconstexprが追加されています。これらは、<complex>もそうですが、プレーンな構造体のように振る舞う型として対応されているように思えます。それらのコンストラクタやメンバアクセスが、ユーザーが作るプレーンな構造体と同様にconstexprになってほしいというのは自然な要求でしょう。

std::tupleについてはarrayやcomplexとは異なり、std::getのmutable参照バージョンもconstexprになっています。なんでそれを、std::arrayやstd::complexに分けてやれなかったんだ！　なんでなんでしょうね。提案されるタイミングの問題だったんでしょうか。

<utility>からはほかにも、std::moveとstd::forward（完全転送）がconstexprになっています。これも、constexpr文脈内での値の変更が可能になったためでしょう。

C++17

`constexpr lambda`

lambda式がconstexprで使えるようになりました。lambda式によって作られるクロージャオブジェクトをconstexpr文脈で呼べるようになり、またそれをconstexpr定数として扱えるようになりました。

lambdaにはキャプチャという機能がありますが、constexpr文脈で使うためにはキャプチャしたものは全てコンパイル時定数である必要があります……当たり前ですが。

とはいえC++17以前でも、constexprコンストラクタを持つクラスはconstexpr文脈で使えましたし、メンバ関数をconstexprにすることもできました。つまり、手動で対応するクラスを書けば、ラムダ式と同じことはできていたわけです。むしろ、このような不必要な回避策を取らなくて良いようににする、というのがmotivationであったようです。*5

`if constexpr`

少しconstexpr関数からは離れますが、関連する機能なので紹介しておきます。

これは、ifの後の条件がコンパイル時定数式である場合に使える機能で、選ばれなかった分岐を実体化しない（実行バイナリに含まない）というものです。

これによって、型特性に応じて使える最高効率のコードを生成するというような関数が簡単に書けるようになりました。具体例としては、IteratorのうちRandomAccess/ContiguousIteratorの場合は+Nを、そうでない場合はループを使ってインクリメントを続ける、というようなコードが簡単に書けます。これ以前は、このような場合には別のタグ型を使ってオーバーロードによって切り替えていました。これは関数呼び出しの階層を増やしてしまうので、一回だけならまだしも、複数個の条件があると非常に大変になります。if constexprによってそれが一つの関数で、しかも普通のifの見た目で書けるのはかなりうれしいことでした。

ライブラリ対応

C++17で追加されたライブラリは、最初からconstexprに（できるものは）なっています。例えばoptionalやvariant、string_viewなどです。もちろんいくらかの制限はあり、例えばoptionalは入っている値を変更することはできません。 anyですら、空のanyを作ること自体はconstexprになっていますね。流石に変更はできないようですが。

基本的にこの時点で、動的メモリ確保や入出力を含まないライブラリで、Cの遺産でないものはほとんどがconstexprになっているようです。ただし<algorithm>がconstexprになるのはC++20を待たなければなりません。

C++20

継承

これまで、仮想関数をconstexprにすることはできませんでした。 C++20では、constexprな仮想関数がconstexprな関数でオーバーライドされていた場合、定数式として使うことができます。ただし、呼び出し側の基底クラスポインタとしてはどの関数が呼ばれる可能性もあるわけなので、オーバーライドしている関数は全てconstexprでなければなりません。

同時に、基底クラスポインタの先にどの派生クラスがあるのかあるのかを知るtype_idとdynamic_castも許可されました。

動的メモリ確保（`new/delete`、`std::vector`と`std::string`）

std::vectorとstd::stringがconstexpr対応し、またnewとdeleteもconstexprとなりました。

もちろん、格納する型はコンパイル時にコンストラクト・デストラクト可能である必要があります。そしてnewのオーバーロードは許可されていません。

一番引っかかりやすい制限は、コンパイル時に確保された領域はコンパイル時に解放されなければならないということです。灰は灰に。塵は塵に。コンパイル時に確保したstd::vectorを実行時に触れられるようにする方法はありません。 std::vectorやstd::stringを作ることはできますが、それはconstexpr関数の内部で使い切らなければならず、std::vectorを返す関数を作って、その戻り値をconstexprにすることはできません。

共用体

unionはメンバのうちの一つだけがアクティブな型です。再代入によってこのアクティブなメンバを切り替えるということが、constexprではこれ以前には許されていませんでした。

しかし、std::optionalやstd::stringはunionを使います。optionalはわかりやすいですが、std::stringはShort String Optimizationのために使っているはずです。std::stringをconstexpr対応させるときに、unionのアクティブメンバを切り替えられないことに気付いたようです。

これによって、std::optionalの代入関数やreset、std::variantへの代入などがconstexprになりました。

文法上の制限緩和

constexpr関数内では、たとえコンパイル時に呼んでいなかろうと、例えばインラインアセンブラやtry-catchを記述してはいけませんでした。constexpr内にtry {}が出てきた時点でコンパイルエラーです。しかし、書くだけなら許してほしい（実行時に呼ばれることもあるのだから）という発想は自然です。

この提案で、try-catchとインラインアセンブラは、書くだけなら許されるということになりました。これにより、if(std::is_constant_evaluated())を使うことで、実行時にはこれらの機能を使い、constexpr文脈で呼ばれた場合にはフォールバックを使う、というようなことが可能になりました。

ただし依然として、constexpr関数内で例外がthrowされるとコンパイルエラーとなります。将来的にはもしかするとcatchできるようになるかもしれませんが。

`consteval`

constexpr関数は、コンパイル時にも実行時にも呼ぶことのできる関数でした。

明らかにコンパイル時以外に呼ぶ必要のない巻数や、コンパイル時以外に呼ばれるべきではない関数も、constexprでは実行時にも呼べるようになります。それらの関数を実行時に呼んでしまうことを自動的に避けたい、あるいは、コメントよりもいい方法で読者に伝えたいという欲求は自然なものです。そしてconstevalはそれを実現します。

提案によると、どうやらstatic reflectionのことが念頭にあったようです。reflectionはコードの情報を使ったコードのことで、例えば今使っている変数のクラスが持っているメンバ変数の名前を全て得る関数であるとか、そういう機能のことです。 C++では静的なリフレクション、つまりコンパイル時にそれらの情報を得てコード生成を行うような機能が議論されており、そのような「コンパイル時以外に呼んではいけない関数」を明示する機能が欲しかった、というのがモチベーションの一つになっているようです。

`is_constant_evaluated`

std::is_constant_evaluated()は、コンパイル時に評価されている（つまり今がコンパイル中である）という場合はtrue、そうでない場合はfalseを返す関数です。これを使ってifで分岐すれば、実行時にしか使えない機能、例えばインラインアセンブラによって狂気的にチューニングされたコードと、コンパイル時にも動く普通のコードを、一つのconstexpr関数内で同居させることができます。実際、この機能のために、constexpr関数の文法上の制限緩和が進んだのでしょう。

ただし、if constexprとこれを組み合わせると、if constexprが評価されるのがコンパイル時であるせいで常にtrueになってしまうという大きな落とし穴があることに注意してください。これはC++23で、if constevalによって解決されます。

`<algorithm>`と`<numeric>`、それに関係したライブラリ機能

基本的に渡されたイテレータ範囲で作業をする<algorithm>の多くの関数は、動的メモリ確保がなくとも（std::arrayがあるので）constexprで実装されていいように思えるものばかりでした。ここで、それらの関数がconstexprになります。

とはいえ<algorithm>をconstexprにするために、いくらか追加の作業が行われていたようです。たとえば、constexprで使えるIteratorの要件が定義されたり*6、swapがconstexpr対応したり*7とところどころが整備されていました。

また、<algorithm>の関数はものによってはコンパイラのイントリンシックや、もっとアグレッシブな場合はアセンブリによって高速化が図られていることがありました。これらの高速化をあきらめてconstexpr対応すると、当然ながら速度が落ちるのではないかということが懸念されていました。

提案では、速度低下が100%起きないと断言はできないものの、速度低下を回避しながらconstexprにできるだろうと述べています。その理由は、

当時既にGCCの__builtin_memcmpはconstexprでも使えるので、コンパイラベンダーが頑張ることで他の組み込み関数、例えば__builtin_memmoveや__builtin_memsetも同様の処置ができるだろう。
アセンブリが使われている部分も、コンパイラのイントリンシックで置き換えることが可能だろう
外部の関数が使われている部分も、それをインラインに展開するか、あるいはイントリンシックを使って再実装できるだろう
というか最近のコンパイラは賢いのでそういった最適化をヘビーにしている関数はそんなに多くないだろう

ということでした。

この提案によって、<algorithm>と<numeric>にある多くのアルゴリズムがconstexprになりました。ここで見送られたのは、追加のメモリ領域を使う場合があるstable_sortなどのアルゴリズムと、まだconstexprになっていない乱数を使うアルゴリズムであるshuffleとsampleです。

https://www.open-std.org/jtc1/sc22/wg21/docs/papers/2017/p0202r3.html

`<complex>`

かなり今更なのではないかと思うのですが、std::complexの演算がconstexpr対応しました。 isnanなどの<cmath>関数やコンパイラのビルトイン関数が使われていたことが、遅れた原因のようです。というわけで、いくつかの簡単に実装できる数学関数しか使わない演算だけがconstexprになりました。四則演算と、normとconjです。

sqrtなどのより複雑な数学関数を使うstd::complex::absなどの関数は見送られました。

C++23

`if consteval`

ついこの間のアドベントカレンダー記事で紹介されていました。一応説明をしておくと、これはconstexpr文脈にいるかどうかでコードを分けるための機能です。

if (std::is_constant_evaluated()) {/*1*/} else {/*2*/}を使ってコードを分岐させると、分岐は意図した通りにするのですが、実体にはどちらのパスも残ります。もし/*1*/の中にconstevalなコードを持っていた場合、実際には通らないパスとはいえ、実行時に呼びだされる関数のコード内にconstevalが残るため、エラーになってしまいます。

ではこのような場合のために、通らないパスを実体から消し去るif constexprを、と思いたいところですが、if constexprはコンパイル時に処理されるため、is_constant_evaluatedを呼ぶと常にtrueになってしまいます。この問題を避けるため、期待通りに動作するif constexpr (std::is_constant_evaluated())として、if constevalが導入されました。

ちなみにif constevalはC++20に向けた提案でしたが、締め切りを破っていたようです。それが原因なのかは知りませんが（多分そうでしょう）、これはC++23の機能になりました。

文法上の制限緩和

これまでも何度か（try-catchやインラインアセンブラ）ありましたが、C++23でもいくつかの文法機能がconstexpr関数内に存在することが許されるようになりました。

C++23では、constexpr関数内のラベルとgoto、リテラルでない型の変数、static, thread_localな変数の存在が許可されました。ただし評価してしまうとエラーになります。

https://www.open-std.org/jtc1/sc22/wg21/docs/papers/2021/p2242r3.html

もう一つ、constexpr関数内でconstexprではない関数を呼んでいる場合、それが実際に評価されるまではエラーにならないようになりました。

これまで見てきたように、コア言語側でconstexpr実装が可能になったライブラリ機能がそれと同時に実際にconstexprになることは珍しいです。大抵の場合は、1世代遅れてconstexpr指定されます。もしconstexpr指定されていない関数を呼ぶconstexpr関数が、実際に呼ばれていないうちから警告を出していた場合、その警告を止めるために大量の機能テストマクロをconstexpr周辺に置くことになります。これはまあ冗長でしょう。そういうわけで、constexprではないというエラーは、実際に評価されたときに出すようにするということになりました。

https://www.open-std.org/jtc1/sc22/wg21/docs/papers/2022/p2448r2.html

簡単な数学関数

<cmath>の比較的単純な関数、つまりabsやround, ceil, floor、fmodとreminder、fminとfmax、それからfmaに、isfinite, isinf, isnanなどの判定関数、copysign, frexp, ldexp, scalbなどがconstexprになりました。

ただ、gcc以外のコンパイラはあまり対応していないようです（clang-18はダメでした）。

規格への変更がほぼconstexprの追加しかないので、このpaperを見ればどれが対応したのかはすぐにわかります。

https://www.open-std.org/jtc1/sc22/wg21/docs/papers/2021/p0533r9.pdf

C++26

数学関数

<cmath>と<complex>に入っているほとんどの数学関数がconstexprになります。これで、sqrtやsin, cosなどの普段使いの数学関数がconstexprになります。

https://www.open-std.org/jtc1/sc22/wg21/docs/papers/2023/p1383r2.pdf

これで概ね、入出力を除くすべてのピースが埋まったように思えます。シミュレーションやデータ解析などの計算で閉じているプログラムは、ほとんどがconstexprで簡単に動くようになったのではないでしょうか。

型消去

void*を通した型消去というテクニックがあります。 C++26では、これを行うためにconstexpr文脈内でのvoid*から別の型のポインタT*へのキャストが許可される予定です。比較的知名度が低いテクニックのように思われるので、少し解説しておきます。

std::functionやstd::anyなどの「どんな型でも入る」クラスはこれを使って実装することができます。

std::anyのようにユーザーが取り出すべき型を知っていると思ってよい場合は、対象を格納する際にvoid*にキャストし、取り出す際にtemplate引数としてユーザーに型情報を教えてもらってそれにキャストして返します。std::any_cast<T>がそれに相当します。*8

std::functionのようにユーザーは取り出すべき型を知らない（忘れてよい）代わりにするべき操作が決まっている場合は、void*を適切にキャストして目的の操作をする関数への関数ポインタを覚えておくことでこれを実装できます。つまり、オブジェクト指向の説明でよくある Animal::speak() を例とすると、

class Cat
{
  std::string_view speak() const noexcept {return "meow";}
};

class Animal
{
  using func_type = std::string_view (*)(const void*);
  func_type speak_impl;
  const void* animal;

public:
  template<Speakable A>
  Animal(const A& a)
    : animal(std::addressof(a)),
      // 最初の型に戻してメンバを呼ぶ方法をここで作って覚える
      speak_impl([](const void* any) {
        return static_cast<const A*>(any)->speak();
      })
  {}

  std::string_view speak() const noexcept
  {
    return this->speak_impl(animal);
  }
};

のようにすれば、元の型に戻して対象のメンバ関数を呼ぶ関数を覚えておくことができ、ユーザーはもとの型Aを覚えておいて渡してやる必要がありません。

これだけでも便利ですが、他にも嬉しいことがあります。型消去をtemplateの代わりに使うことで、実体化されるコード量を削減できるという点です。templateの場合は型引数ごとに異なる実体が生成されてしまい、executableが大きくなりがちですが、型消去を使えば実体を一つになり、これを小さくすることができます。

これをconstexpr中でもできるようにしたいという提案がC++26に入る予定です。

https://www.open-std.org/jtc1/sc22/wg21/docs/papers/2023/p2738r1.pdf

`<algorithm>`で前回スルーされていたもののいくつか

C++20時点で<algorithm>のほとんどの関数はconstexprだったのですが、一部の関数はそこに含まれていませんでした。それら取り残された関数のうち、std::stable_sort, std::stable_partition, std::inplace_mergeがconstexprになる予定です。

これらはもともと、作業用のメモリを動的に確保したり、そこにplacement newするような操作を行うために後回しにされていました。*9 しかし既にconstexprで動的メモリ確保が可能になった以上、阻むものはなくなった形です。

https://www.open-std.org/jtc1/sc22/wg21/docs/papers/2022/p2562r1.pdf

TMP

脱線ではありますが、template metaprogramming (TMP) についてもごく軽く説明しておきます。

TMPでは、再帰によって繰り返しを、（部分）特殊化のパターンマッチによって条件分岐を実現することで、templateの実体化を通して何らかの計算をすることを指します。

伝統に則って、素朴な素数判定を書いてみましょう。

namespace detail
{
template<std::uint32_t N, std::uint32_t I>
struct is_prime_impl
{
  constexpr static bool value = ((N % I) != 0) &&
    is_prime_impl<N, I-1>::value;
};

template<std::uint32_t N>
struct is_prime_impl<N, 1>
{
  constexpr static bool value = true;
};
} // detail

template<std::uint32_t N>
struct is_prime
{
  constexpr static bool value = detail::is_prime_impl<N, N-1>::value;
};
template<>
struct is_prime<1>
{
  constexpr static bool value = false;
};
template<>
struct is_prime<0>
{
  constexpr static bool value = false;
};

is_prime<N>::value には、Nが素数の場合trueが、そうでない場合falseが入ります。どのような仕組みか見てみましょう。まず、このis_prime<N>::valueは以下のようになっています。

template<std::uint32_t N>
struct is_prime
{
  constexpr static bool value = detail::is_prime_impl<N, N-1>::value;
};

ここで、実際の値はdetail::is_prime_impl<N, N-1>::valueであることがわかります。そちらを見てみましょう。

template<std::uint32_t N, std::uint32_t I>
struct is_prime_impl
{
  constexpr static bool value = ((N % I) != 0) &&
    is_prime_impl<N, I-1>::value;
};

ここでは、NがIで割り切れるかどうかの値と、再帰的に展開されるis_prime_impl<N, I-1>::valueとの&&が取られています。再帰部分では、Nはそのまま、Iは1ずつ減らして次の繰り返しに入っていることがわかります。この再帰がI == 1のときに止まるべきなのはすぐにわかるでしょう。1は何でも割り切るので、常に(N % I) == 0になってしまいます。再帰をI == 1で止めるのは、この部分です。

template<std::uint32_t N>
struct is_prime_impl<N, 1>
{
  constexpr static bool value = true;
};

これは「部分特殊化」と言って、第二template引数が1のときにマッチする型です。これにより、I == 1となった場合はis_prime_implの実体はこちらになり、再帰展開は止まる場所を見つけます。そしてここで変える値はvalue = trueなので、ここまでが全てtrue、つまりN % I != 0だった数は、true && true && .. && true = trueとなります。

また、これだとN == 1やN == 0だったときに困ります。なので、is_primeにはその場合のための特殊化を用意しておきます。

template<>
struct is_prime<1>
{
  constexpr static bool value = false;
};
template<>
struct is_prime<0>
{
  constexpr static bool value = false;
};

このように、再帰展開による繰り返しと、特殊化・部分特殊化によるパターンマッチを使うことで、テンプレートクラスの実体化を使って計算を行うことができます。

もちろん計算の対象は値だけでなく、using/typedefを使って型を出し分けることも可能です。これと関数オーバーロードを組み合わせることで、特定の条件を満たす型（例：Iteratorのiterator_traits<Iterator>::iterator_categoryがRandomAccessIteratorであるもの）が来た場合にのみ関数の実装を分ける、というのは頻出のパターンになっています。もちろん、現代ではこのようなことはConceptによって解決が可能となり、徐々に過去のものとなっていくでしょうが、過去の資産を紐解く際には便利な知識になるでしょう。

C++23でのコンパイル時レイトレーシング

一口にレイトレーシングと言っても、どこまでやるのかというのは難しい問題です。

今回は、非常に有名でありかつ既に多くの人が走ったことのあるレギュレーション、つまり"Ray tracing in one weekend"を走っていこうと思います。

https://raytracing.github.io/books/RayTracingInOneWeekend.html

この教材もC++を使ってはいますが、何～故～か、実行時に走るコードしか書かれていないので、やる意味はあるでしょう。

とはいっても時間的な猶予と計算機リソースの問題があるので、最後のページの100個以上の球体が並ぶ画像まではいきません。中盤の、diffusive/metallic/dielectricなmaterialが適用された球体が並んでいるところまでとします。実際、そこまでたどり着けば後は実行時間の問題でしかないと言えなくもないでしょう。*10

実際に出力された画像は以下の通りです。

コンパイル時計算で生成した画像。このクオリティだとコンパイル時間は大体30分程度。

画像ファイル出力

ファイルの入出力は流石にコンパイル時にはできません。よって、ファイルのバイト列をコンパイル時に作っておいて、実行時にはそれがファイルに出力されるだけ、という状況にしておきたいところです。

std::vectorやstd::stringがconstexpr対応したとはいえ、コンパイル時に作ったstd::vectorを実行時に触ることはできません。コンパイル時に作られたstd::vectorは、コンパイル完了と同時に解放されなければなりません。ですので、ファイルはstd::array<std::uint8_t, N>にしておき、この先頭をconst char*として出力することにしましょう。

最初はppmのP3を使っており、数値を文字列に変換する関数を書いていましたが、どのコンパイラもconstexpr内で実行できる計算の回数に上限があるので、ここでそれを消費するのはまずいと考えP6を使うことにしました。 P6だとバイト単位でRGBが書き込まれるので、変換は必要ありません。計算回数上限とメモリ使用量がほとんど唯一の縛りだったように思います。

std::arrayのサイズは関数内で決めて（もちろん定数ですが）、返り値はautoにしておきます。

constexpr auto
make_ppm(const std::array<pixel, IMAGE_SIZE_X * IMAGE_SIZE_Y>& image)
{
    constexpr auto header_string =
        "P6\n" STRINGIZE(IMAGE_SIZE_X) " " STRINGIZE(IMAGE_SIZE_Y) "\n255\n";
    constexpr auto header_size = std::string_view(header_string).size();
    constexpr auto pixel_size = 3; // [byte]
    constexpr auto ppm_size = header_size +
        (IMAGE_SIZE_X * IMAGE_SIZE_Y * pixel_size);

    std::array<std::uint8_t, ppm_size> retval;
    for(std::size_t i=0; i<header_size; ++i)
    {
        retval[i] = static_cast<std::uint8_t>(header_string[i]);
    }
    std::size_t idx = header_size;
    for(std::size_t pxl=0; pxl<IMAGE_SIZE_Y * IMAGE_SIZE_X; ++pxl)
    {
        const auto [r, g, b] = image[pxl];
        retval[idx++] = r;
        retval[idx++] = g;
        retval[idx++] = b;
    }
    return retval;
}

これが成功しているかどうかは、出てきたバイナリを見るとわかります。 xxdで見てヘッダのP6を検索してみると……。

実行バイナリをxxdで見ているところ。.rodataセクションにPPM画像のヘッダが入っており、おそらく画像本体と思しきバイト列が続くことが見て取れる。

となり、バイナリに実際に画像データが埋め込まれていることがわかります。

数学関数

レイトレーシングではベクトルの距離を計算する必要があるため、sqrtは必須です。 $1 / \sqrt{x}$ を計算するrsqrtがあってもよいでしょう。

sqrtのような数学関数がconstexprになるのはC++26からなので、C++23では使えません。これに関しては自力でどうにかする必要があります。今回はC++23でも使える<cmath>関数であるldexpとfrexpを使って浮動小数点数を指数部と仮数部に分解し、仮数部を256分割してそれぞれの区間を2次関数で補完することにしました。

別のコードでパラメータを生成しておけば、2次関数の計算は本当にやるだけです。

constexpr inline std::size_t sqrt_N = 256;
constexpr inline double sqrt_dx = (1.0 - 0.5) / sqrt_N;
constexpr inline double sqrt_a[sqrt_N] = {
#include "parameters/sqrt_a.dat"
};
constexpr inline double sqrt_b[sqrt_N] = {
#include "parameters/sqrt_b.dat"
};
constexpr inline double sqrt_c[sqrt_N] = {
#include "parameters/sqrt_c.dat"
};

constexpr double sqrt_interp(const double x)
{
    const std::size_t i = (x - 0.5) / sqrt_dx;
    const auto a = sqrt_a[i];
    const auto b = sqrt_b[i];
    const auto c = sqrt_c[i];
    return (a * x + b) * x + c;
}

sqrtの場合、指数部は単に半分にするだけで計算できます。奇数だった場合は、最後に余った1に相当する $\sqrt{2}$ をかける必要があることに注意しましょう。また、指数が負だった場合には逆に割らなければなりません。 infやnanの場合についても、C++23時点で既にisinfやisnanがconstexprなので特に問題はありませんでした。

現実的には、clangがfrexpとldexpに対応していないので、これを実装する必要があります。とはいえstd::bit_castがconstexprなので、doubleをstd::uint64_tに変換したのちビット演算で指数部と仮数部を取り出して、仮数部を[1, 2)から[0.5, 1)に変換すればよいだけなので、自作は容易です。

指数部が負になっている場合などの扱いをかなり愚直にやったので長くなってしまっていますが、以下のようになります。

constexpr double sqrt(const double x)
{
    if(x == 0.0 || x == -0.0)
    {
        return 0.0;
    }
    if(std::isnan(x))
    {
        return std::numeric_limits<double>::quiet_NaN();
    }
    if(std::isinf(x))
    {
        return std::numeric_limits<double>::infinity();
    }

    int ex=0;
    const double norm = std::frexp(x, &ex);

    const int zex = ex / 2;
    if(ex >= 0)
    {
        if(ex % 2 == 1)
        {
            const double z = sqrt_interp(norm) * std::numbers::sqrt2;
            return std::ldexp(z, zex);
        }
        else
        {
            const double z = sqrt_interp(norm);
            return std::ldexp(z, zex);
        }
    }
    else
    {
        if(ex % 2 == -1)
        {
            const double z = sqrt_interp(norm) / std::numbers::sqrt2;
            return std::ldexp(z, zex);
        }
        else
        {
            const double z = sqrt_interp(norm);
            return std::ldexp(z, zex);
        }
    }
}

乱数

<random>はconstexpr対応していないので、乱数に関しては自分で作る必要があります。そこまで高品質のものを求めているわけではないので、簡単にxorshiftでよいでしょう。

struct xorshift64
{
    std::uint64_t state;
};

constexpr xorshift64 next(const xorshift64& curr) noexcept
{
    std::uint64_t x = curr.state;
    x ^= x << 13;
    x ^= x >>  7;
    x ^= x << 17;
    return xorshift64{x};
}

どちらかというと問題はここよりも、これをdouble上の乱数にすることです。とりあえず[0, 1)の一様乱数が作れるとほとんどのことが何とかなるので、これを作ります。

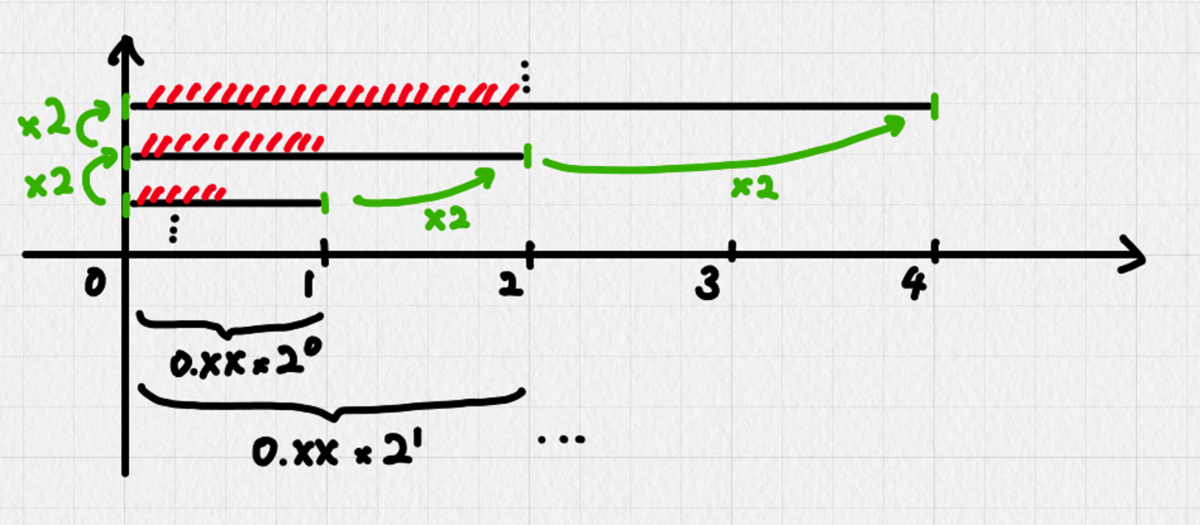
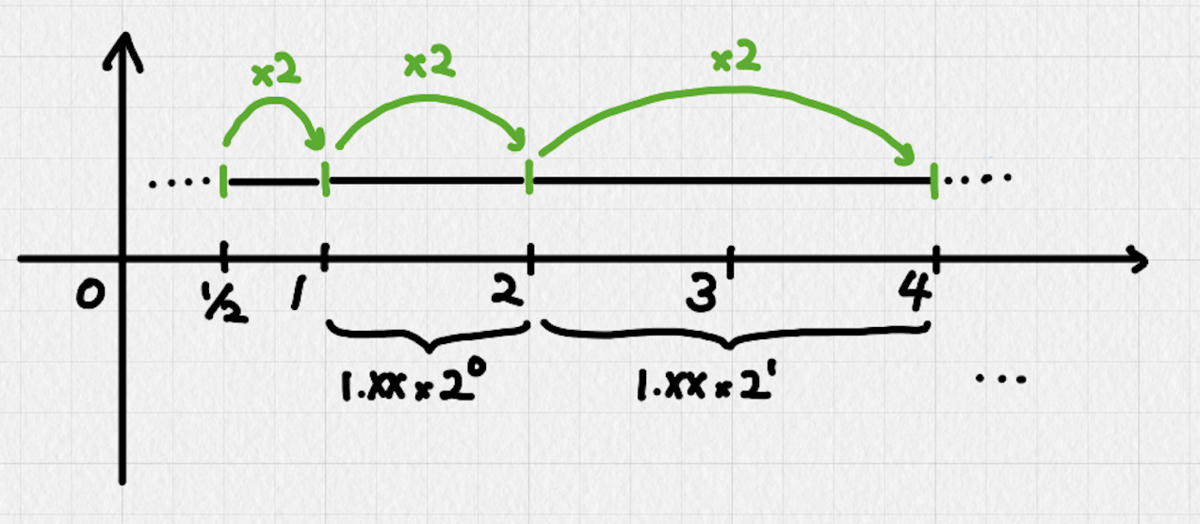
今回は簡単に、指数部を0に固定して仮数部を乱数にすることで[1,2)の乱数を作り、ここから1を引いて[0, 1)にすることにします。これだと得られる値が仮数部の最小単位―doubleだと2^-52―刻みになるので、本来指数部を小さくすると表現できるはずのより小さな値が表現できないという問題がありますが、今回は特にそこは必要がないので、ここで切り上げます。

std::bit_castは最初からconstexprなので、uint64_tで作ったビット列をそのままdoubleに変換することができます。

constexpr std::pair<double, xorshift64> uniform_12(const xorshift64 rng) noexcept
{
    static_assert(std::numeric_limits<double>::is_iec559, "assuming IEEE 754");

    const auto nrng = next(rng);

    const std::uint64_t mantissa_mask   = (1ull << 52) - 1;
    const std::uint64_t random_mantissa = nrng.state & mantissa_mask;
    const std::uint64_t exponent_bias   = 1023ull << 52;
    const std::uint64_t float64         = exponent_bias + random_mantissa;

    return std::make_pair(std::bit_cast<double>(float64), nrng);
}
constexpr std::pair<double, xorshift64> uniform_01(const xorshift64 rng) noexcept
{
    const auto [d, r] = uniform_12(rng);
    return std::make_pair(d - 1.0, r);
}

勢い余ってxorshift64自体を毎回更新していますが、別に変更しながらでもよかったですね。まあ特に変わりはありませんが……。

浮動小数点数については以前に記事を書いているので、どういう表現になっているのか知らないという人はこちらもご覧ください。

in-neuro.hatenablog.com

オブジェクトのマテリアル

レイトレーシングにおいてオブジェクトには、位置と形状の他に、それに光が反射したときに反射光の色がどう変化するかの値と、どの方向に光が反射するかの情報が入っています。色は単純にRGBがそれぞれどの程度減るかという情報で管理されていますが、光の反射は分布も計算方法もかなり異なるので、異なる関数を呼び分ける必要が生じます。

オブジェクトによって同じ名前の関数の振る舞いを変える方法は大きく分けて二つあります。std::variantと継承です。継承もC++23ではconstexprで使えるのですが、今回は単純な好みでstd::variantを使いました。

std::visitを使ってconstexpr lambdaでオーバーロードされているscatter関数を呼べば、マテリアルに応じたscatter関数が呼ばれます。

struct object
{
    color attenuation;
    std::variant<diffusive, metallic, dielectric> material;
    std::variant<sphere> shape;
};

template<std::size_t N>
constexpr std::pair<color, xorshift64>
ray_color(const ray& r, const world<N>& w, const xorshift64 rng, const std::size_t depth)
{
// ...
        const auto [nray, nrng] = std::visit([&r, &collision, rng](const auto& mat) {
                return scatter(r, collision, mat, rng);
            }, obj.material);
// ...
}

実行

g++-13とclang++-18を使って実行しています。コンパイル時計算をするにあたっては、どちらも一長一短あります。

例えば、gccとclangはどちらもコンパイル時間が長くなりすぎないようにコンパイル時計算で許す計算の回数を絞っているのですが、この回数の上限が異なります。gccは-fconstexpr-ops-limit=Nで、clangは-fconstexpr-steps=Nでこの上限を変更することができます。できるのですが、gccは2^32-1を超えても問題ないのに対して、clangは2³²以上の値を指定することができません。よって、clangの公式バイナリでのコンパイル時計算はgccと比べると著しく制限されています。ただし、この制限解除には多くの人が取り組んでおり、以下のような変更を加えることでこの上限を解除したclangをビルドすることができます。*11

qiita.com komorinfo.com

また、clangではldexpやfrexpがconstexprになっていないなど、マイナーな部分とはいえgccと比べて少し対応が進んでいない部分があります。

ではgccを使っておけば何の問題もないのかというと、そうでもありません。確かにgccではconstexprでの評価回数制限がかなり緩いのですが、代わりにすさまじいまでのメモリを消費します。内部的に定数式の値を全て覚えているのでしょうか？　秒間数百MBのペースでメモリ使用量が増えていき、今回の最後の画像を生成する時は128GBを突破してしまいました。これ以上のメモリを積んだマシンは用意できなかったので、gccを使っても無制限にコンパイル時計算ができるということはありません。

というわけで、おそらく最善の方法はパッチを当てて-fconstexpr-stepsの上限を解除したclangを使うことだと結論付けられます。

実際のコード

コードは以下で公開しています。

github.com

コンパイルに時間がかかりすぎるので、CIを設定する気になれませんでした……。

おわりに

ちょっとコードがあまりにも普通になったのでconstexprで縦軸でまとめるか、と思ったら非常に大変なことになってしまい（見通しが甘すぎる）、クソ長くなった上に死ぬほど遅れました。とはいえ、たまに自分でもどこまでがconstexprで使えるかを覚えていないことがよくあったので、いい機会だったと思います。実際には（特にライブラリ機能に）見落としがあると思いますし、ひょっとすると誤解してるものもあるかもしれません。その場合はあとで更新するかもしれません（した場合は一番上に書いておこうと思います）。

書いてみると、C++23ではコンパイル時計算はほとんどもう普通のコードになっていることがよくわかります。事実、入出力と乱数や数学関数などがまだ対応していない、ということを念頭に置いて普通のコードを書くと、それがそのまま動くというような状態でした。

一番最初に一回計算しておけば済むことを先に計算する、というような目的で使っている場合、数学関数を除けばほとんど障害になるものはないでしょう。制限だらけだったころのことを思うと少し……なんというか……面白くなくなったという気はしますが、実際に書かないといけないコードを書いているときは楽に書けた方が良いに決まっているので。便利な時代になったと思います。

*1:Erwin Unruh, http://www.erwin-unruh.de/

*2:Item 48: Be aware of template metaprogramming. Effective C++: 55 Specific Ways to Improve Your Programs and Designs, Scott Meyers

*3:History of TMP, C++ Programming/Templates/Template Meta-Programming, https://en.wikibooks.org/wiki/C%2B%2B_Programming/Templates/Template_Meta-Programming#History_of_TMP

*4:https://dlang.org/spec/function.html#interpretation

*5:https://isocpp.org/files/papers/N4487.pdf

*6:https://www.open-std.org/jtc1/sc22/wg21/docs/papers/2018/p0858r0.html

*7:https://www.open-std.org/jtc1/sc22/wg21/docs/papers/2018/p0879r0.html

*8:格納する際に簡単なのは動的メモリ確保をしたのちそこへのポインタをvoid*にすることでしょう。実際の std::any は、Small String Optimizationに似た最適化によって動的メモリ確保を回避しています

*9: III C. Analysis of existing algorithm implementations. https://www.open-std.org/jtc1/sc22/wg21/docs/papers/2018/p0879r0.html

*10:とはいえそこはコンパイル時計算では結構本質的に重要な問題ではあるのですが……。

*11:今回やろうと思っていたのですが時間がとれずできませんでした……。

2022-01-05

一人growiでvimのkeymapをやる

少し前に昼食を食べながら調べてたらdevelopper toolのconsoleでCodeMirror.Vim.map(...)をやればできることに気付いてそのままブックマークレットにしたのだが、手元で作業しながらたびたび編集していたら押すのが面倒になってきたのでもうちょっとだけ調べた。

やり方

管理画面のカスタムスクリプトに以下を書く。

window.addEventListener('load', (event) => {
  if (!window.CodeMirror || !CodeMirror.Vim) {
    console.log("[warn] no CodeMirror")
    return
  }

  CodeMirror.Vim.unmap('<Space>');
  CodeMirror.Vim.map('<Space><Space>', 'l');
  CodeMirror.Vim.map('<Space>h', '0');
  CodeMirror.Vim.map('<Space>l', '$');
  CodeMirror.Vim.mapCommand('jk', 'action', 'exitInsertMode', {}, {context: 'insert'});
  // ...好きなだけ
})

これだと全員に適用されるだろ

そんな気がする。今これをやっているgrowiは自分専用のメモなので、これで十分と判断してこれ以上やらなかった。

なんで最初に`<Space>`を`unmap`してるの？

手元ではleaderに<Space>を使っているので、<Space>lとかに$をマップしたかった。すると、CodeMirrorではデフォルトで<Space>がlにマップされているので、<Space>lを全体としてマップすることができない。なので一度<Space>をunmapする。すると、<Space>直後に何かが来るものをマップすることができる。

possible vim leader key work-around? - #4 by benhormann - discuss.CodeMirror

ということがここに書いてあった。

最後の長いの何？

なんか<Esc>にマップしようとしたら上手くいかなかったので直接exitInsertModeに対してマップした。そういうこともできますよというメモ。

初期はjjに<Esc>をマップしていたのだけど、何度も連打していると人差し指にそこそこの負荷がかかったので今はjkを<Esc>にマップしている。連打よりも人差し指→中指の方が速いし疲れない。大抵勢い余ってjklと打っているがlは無害なので問題になっていない。

連打よりは文中に登場しそうだが、今のところDijkstra以外で困ったことはない。 Dijkstraの大ファンで毎日感謝の写経1万回をやってる人は別のものにマップした方が良いと思う。

個人用メモにgrowiってオーバースペックじゃない？

そうかも。

ラボではcrowiをオンプレで立ち上げて管理とかしてたので管理も書き方とかも慣れていたというのはある。慣れていたのはcrowiにだけど。それにgrowiはdocker-composeでやったからcrowiで個別のサービスを管理してたときに苦労したような問題は何一つ起きなかったけど。

ユーザーごとにマッピングを変える場合はどうするべきだろう。まあ順当に、ユーザーのホーム以下にvimrcみたいなページを用意して、そこにmap x yみたいなのを書かせて、それを取得してパースして実行という形になるだろうか。

load後に使えるappContainerにはcurrentUsernameが入っているので、ユーザーのホーム以下の決まったページへのパスはすぐにとれるはず。内容の取得はわからないけど、普通は何かしらのAPIがあるんじゃないだろうか。パースはちゃんとやると面倒だが、map x yだけの簡単なものなら一瞬でできそう。

できそうなんだけど、Web周りに慣れていないので時間がかかりそうだったし、自分しか使ってないので必要性がないためにやらなかった。

うーんWeb関係のことをほとんど何一つやったことがない（古の時代に人が作ったWebサイトに手打ちしたHTMLとかごく簡単なスクリプトを足したりしたくらい）のが地味に色んなところで効いてくる。ちゃんと勉強した方がいいんだろうけどな。

2021-12-15

可変長テンプレートでもstd::source_locationを使いたい！

この記事はC++アドベントカレンダー2021の記事です。

qiita.com

小ネタですが今日の分が埋まっていなかったので。

`std::source_location`とは

std::source_locationは、その名の通りソースコード中の位置を表す情報が入った構造体です。C++20以降で使うことができ、<source_location>で定義されています。

https://cpprefjp.github.io/reference/source_location/source_location.html

__FILE__や__LINE__のモダンないいかんじのバージョンだ、という認識でだいたいOKです。

この構造体は普通、std::source_location::current()で作ります。この関数は呼ばれた位置を示すstd::source_locationを返します。デフォルトコンストラクタもありますが、コンテナに入れるときに気を使わなくていいくらいの用途しかないと思います。

明示的にstd::source_location::current()を呼ぶのは書くのも意識するのも面倒なので、ほとんどの場合において、これは関数のデフォルト引数として使います。この機能のいいところは、それでも意図した通りに動くところです。

void f(std::source_location loc = std::source_location::current()) {
    std::cout << "in function " << loc.function_name()
        << " at " << loc.file_name() << ":"
        << loc.line() << ":" << loc.column() << std::endl;
}

f(/*この中でcurrent()が呼ばれるので、この位置が出力される*/);

ログ取りに便利ですね。

この構造体はコピー構築・コピー代入ができるので、持ちまわることもできます。たとえば

class X {
  public:
    X(std::source_location loc = std::source_location::current())
        : loc_(loc)
    {}
  private:
    std::source_location loc_;
};

のようにしておくと、Xを構築した箇所の情報を追跡することができます。

問題

上記のようにsource_locationはデフォルト引数として使われることが多い、というか、あまり手動で構築する機会はありません。ですが、デフォルト引数が使えない場所というのはあります。可変引数テンプレートです。

まず、デフォルト引数は省略される可能性があるため、前にも後ろにもあるとどの引数がどれに対応するのかあいまいになります。なので省略不可能な引数は全て、省略可能なものの前に定義しなければならないと決まっています。

int f(int a = 10, int b, int c = 30); // error!
f(10, 20); // a = 10 ? b = 10 ?

可変引数テンプレートは、任意個の引数にマッチすることができるため、始まって以降全ての引数を吸い尽くします。つまり、可変引数テンプレートの後に何かを明示的に渡すことはできません。¹

template<typename ... T>
int f(T&& ... args, double x); // error!

よって、デフォルト引数はそれ以外の引数よりも後ろに置かなければならないものの、可変引数テンプレートはそれ以外の引数よりも後ろに置かなければならない、というわけでこの二つは競合します。

template<typename ... T>
int f(T&& ... args, // error!
      std::source_location loc = std::source_location::current());

ですが、特にログなどの用途では可変引数テンプレートは便利です。なんとかこれらを同時に使えないものでしょうか。

解決方法

今回の問題は、可変引数テンプレートとデフォルト引数が同じレイヤーに登場していることに起因しています。方針としては、この二つが登場するレイヤーを分ければよいということになります。

そこで、「関数のように見えるが実は違うもの」として自然にクラスを思い浮かべます。ですが、クラスのoperator()だと、クラスの初期化が終わっていなければなりません。クラスの初期化が終わっているということは、クラステンプレートは実体化されているということです。これだとコンストラクタ呼び出しのために余計な括弧が必要ですし、可変引数テンプレートもコンストラクタ呼び出し時に明示的に与えなければなりません。

なら、コンストラクタ呼び出しを使うのはどうでしょう。これならとりあえず第一の問題、コンストラクタのための余計な括弧が必要になることは解決し、見た目上は普通の関数にしか見えなくなります。

さらに、クラスのテンプレート引数に可変引数テンプレートを押しやっておけば、コンストラクタ内では引数のリストが既知になります。するとコンストラクタでデフォルト引数を使えるようになり、可変引数テンプレートとデフォルト引数が競合することはなくなります。

template<typename ... Args>
class f {
    // ここではすでにArgs...は既知（f<Args...>のコンストラクタだから）
    f(Args ... args, std::source_location loc = std::source_location::current()); // OK!
};

これを関数であるかのように書けるよう、（自明な）推論補助を書きます。コンストラクタがクラスのテンプレートパラメータ型の値を直接受け取っているのでなくてもいけるやろと思ったら無理でした。

template<typename ... Args>
f(Args...) -> f<Args...>

ここではデフォルト引数は書きません。²

このようにすると、以下のコードが通ります。

f(42, 3.14, "foobar"s);

これは、あたかも関数呼び出しに見えますが、実際にはf<int, double, std::string>のコンストラクタを呼んで、できたfのインスタンスを即捨てるコードです。この時点で、コンストラクタに副作用を持たせることによって副作用のあるvoidを返す関数は実現できます。

では値を返せるようにしましょう。受け取ったものから必要なものを計算して、メンバとして持ちます。どうせfがクラスであることを知っているのは我々だけなので、暗黙の型変換ができるようにしましょう。

template<typename ... Args>
class f {
    f(Args ... args, std::source_location loc = std::source_location::current())
      : result(do_something(args...))
    {
        std::cout << "at " << loc.line() << ":" << loc.column() << std::endl;
    }
    operator int() const noexcept {return this->result;}
  private:
    int result;
};
template<typename ... Args>
f(Args...) -> f<Args...>

const int a = f(42, 3.14, "foobar"s);

というわけで、可変引数テンプレート関数でstd::source_locationを使っているように見せかけるコードでした。もし返り値をautoで受けられるとこのfがそのまま受け取られるのでバレないように祈る必要が出てきます。あとコピーが重いものは適切にmoveしたりするなんかうまくやる必要があります。

また、代入時の変換は継承でも実現可能です。もしテンプレート周りでややこしくなっていたら試してみるのも手でしょう。

書く前に10秒だけ調べたら新規性がなかったようですが（ https://stackoverflow.com/questions/57547273/how-to-use-source-location-in-a-variadic-template-function ）、深く考えないことにしました。

ほかにいくつか試しましたが、これはというものは考え付きませんでした³。なんかもっといいアイデアはないもんでしょうか。

限定付きのよりよい解決策

例えば、関数の第一引数が確定している場合は、その第一引数を適当にラップすることで実装可能です。例えば、ログ用の関数でlog_levelを取ることにしましょう。

enum class log_level {debug, info, warn, error, fatal};

// invalid
template<typename ... Args>
void log(log_level, Args... args, std::source_location loc = std::source_location::current())

log_levelとsource_locationを持つ適当な構造体を作って、そのコンストラクタでcurrent()を取ることにします。

struct log_level_with_location {
    log_level_with_location(log_level l,
        std::source_location loc = std::source_location::current())
        : lv(l), loc(loc)
    {}
    log_level lv;
    std::source_location loc;
};
template<typename ... Args>
void log(log_level_with_location lv, Args... args);

こうすれば、log(log_level::info, args...)の呼び出しの際にlog_levelからlog_level_with_locationへの変換が発生して、log_level_with_locationのコンストラクタでsource_location::current()が呼ばれます。このコンストラクタはlog(lv, args...)呼び出し時に呼ばれるので、log(lv, args...)時点での位置が取得できます。

もし第一引数が決まっているのなら、これがいいですね。

一応、メタプログラミングによって最後（からN番目）の引数だけを取り出して何かをすることは可能です（参考→ https://in-neuro.hatenablog.com/entry/2020/05/24/171047 ）。このようにすれば、「最後の要素に特定のものを渡しているかどうかチェック」して「最後の要素を特別扱いする」ことが可能ですが、今回はデフォルト引数を渡したいので、これではうまくいきません。関数のdeclarationの時点でデフォルト引数を書く方法が必要です。↩
昔@onihusube9さんに教えていただきました → https://twitter.com/onihusube9/status/1447973137916710917?s=20 ↩
思いつくままに検討した方法ですが、lambdaの初期化captureだとlambdaの宣言箇所に、非型template引数ではtemplateの箇所になってしまうので、うまくいきません（templateは実体化された箇所になってくれないかと期待していましたが……）。すべての可変長引数Tに対してstd::source_locationとTを持つ構造体value_with_location<T>を考えて、それをTから作るコンストラクタでstd::source_location::current()を呼ぶというごり押しは通りそうですが、value_with_location<T>のTの推論がうまくいきません。だからといって型消去をすると型を戻せなくなり、詰みます。↩

2021-10-20

作って理解する浮動小数点数①　基本編

浮動小数点数

以前も浮動小数点数の記事を書いた（作る側の気持ちで理解する浮動小数点数 - in neuro）。だがその時は、浮動小数点数に関するアイデアの説明しかしておらず、実際の「浮動小数点数（IEEE754）」については説明しなかった。今回の記事の目的は、実際の浮動小数点数についてちゃんと解説し、またいくつかの演算をビット単位で自力で書くことで、理解を深めることである。

現実の浮動小数点数

演算について書くとは言ったが、その前に少し浮動小数点数についての基本的なアイデアをおさらいしておこう。このあたりの知識は演算を理解する際にも必要になる。すでに知っている人には退屈だろうから、演算編で引っかかったときだけ見るのでも構わない。

浮動小数点数の基本的構造

浮動小数点数はその名の通り、小数点の位置が動的に変わる数である。基本的な表現方法は1.234x10^-5のような指数表記と同様だ。

例えば単精度（32bit）浮動小数点数のフォーマットは、以下のようになっている。1.234x10^-5のバイナリ表現を見てみよう。

|0|0110'1110|100'1111'0000'0111'1110'0101|
 | '-+-----' '-+------------------------'
 |   |         +-> 23-bit mantissa（仮数部）
 |   +-> 8-bit exponent（指数部）
 +-> sign bit（符号）

一番最初のビットは符号ビットであり、これが0だと正の数、1だと負の数である。よってこれ以降の部分は、表す数の絶対値を決めている。

続いて8bitの指数部がある。ここでは2^-17を表している。これは符号なし整数なのだが、負の値を表現するためにバイアスという値を使う。単精度浮動小数点数の場合はバイアスは-127であり、この8bitを符号なし整数として解釈したものから127を引いた値が指数として扱われる。なので、今回は0b01101110 = 110 (decimal)から、指数は-17となる。

さらに、指数部には特別な値があり、最大（0b1111'1111）と最小（0b0000'0000）の場合には特殊な値を表す。詳しくは、のちの「非正規化数」と「非数と無限」を参照されたい。

残りの23bitは仮数部である。ここでは1.1001111...の部分を表している。2進数なので、0.1は1/2であり、0.01は1/4だ。仮数部の最初のビットは1の位ではなく1/2の位で、続くビットは1/4の位, 1/8の位, 以下同様となる。では仮数部は0.xxxとして[0, 1)の範囲を表現しているのかというとそうではなく、仮数部は1.xxxのxxxの部分を表現している。つまり、1の位に暗黙の1が存在しており、実際に表現している範囲は[1, 2)ということになる。

1の位より上の位を持たず、1の位が非ゼロになるように指数を調整した指数表記を正規化数と呼ぶ。そして浮動小数点数は基本的に正規化されている。例えば1.0110x2³は正規化されているが、0.1011x2⁴は正規化されていない。2進数では非ゼロな数というのは必ず1になるので、常に非ゼロである1の位は効率化のため符号化の際に省略されている。これはケチ表現と呼ばれる。

なぜ1から2の範囲なのか

さて、ではなぜ0.xxxではなく1.xxxなのかについて少し考えてみよう¹。そういう風に決まっているとして終わらせてしまうこともできるのかもしれないが、納得は得られない。これは以前の記事でも書いたが、コンパクトに書き直しておく。

まず、前提として我々は二進数を用いており、また指数部と仮数部を分割したというところまでは認めてしまおう。その上で、我々の目標はできるだけ効率よく広い範囲の実数を高精度に符号化することである、ということも同意してもらいたい。この条件で、仮数部が表現する範囲の良さを考えよう。

まず、0.XXXの場合を考えてみる。この場合、仮数部が表現する範囲は最小で0.0000...、最大で0.1111...なので、[0, 1)になる。これに指数を追加することを考えよう。指数が追加されたことにより、全体を例えば2倍した範囲を表現できるようになる。そのような範囲は何から何までになるだろうか？　0.000...0x2から始まり、0.111...1x2までの範囲になるだろう。これは、[0, 2)の範囲ということになる。振り返ってみると、我々はすでに[0, 1)の範囲は指数が0の場合にすでに精度よく表現できている。この上分解能を1ビット落とした表現で[0, 2)の範囲の一部分として[0, 1)の範囲を表現しなおすことにメリットはない。指数が-1の場合も同じで、[0, 1/2)の範囲が[0, 1)の範囲と被ってしまう。被ってしまうということは同じ値の表現方法が複数あるということで、符号化の効率もよくないし、実装上も不都合が多い。

f:id:tniina:20210916210259p:plain — 図 1. [0, 1)の範囲と指数を組み合わせた場合。指数の異なる数が表現する範囲が重なり、効率が悪い。赤色斜線部は、指数が一つ小さい数がすでに表現している範囲を示す。

対して、1.XXXの場合を考えよう。この場合、仮数部が表現する範囲は最小で1.000...0、最大で1.111...1なので、[1, 2)になる。指数が1だった場合は、範囲は[2, 4)になり、指数が0のときの[1, 2)と被らないどころか綺麗に繋がる。逆の場合も同様で、指数が-1なら[1/2, 1)になるため、こちらも綺麗に繋がる。このようにして、被りが生じないまま数直線上の大部分が表現できることになる。

図2. [1, 2)の範囲と指数を組み合わせた場合。指数の異なる値の範囲が過不足なく繋がる。

この性質は、範囲を[a, b)とし、基数をrとした場合、a * r = bが成立していればどのような組み合わせでも生じる。もし電子回路が-1, 0, 1の3状態で動いていたなら、基数は3になり、範囲は[1, 3)になっていただろう。……いや、ビットが3状態でそれぞれ {-1, 0, 1} の場合は符号ビットが存在しないから（ビット単位で正負があるので）、素直に(-1, 1)の範囲だろうか？　いやそれだと範囲が被ってしまう。仮数部にバイアスをつけて2±1にすればいいのだろうか。これなら3倍して6±3にすると綺麗に繋がるが、範囲内に負の値を含まないようにしたので符号ビットが必要になり、符号ビットがゼロの場合が無駄になってしまう。無駄にしないようにするには、符号ビットがゼロの場合にゼロと非数・無限大を詰め込めばいいだろうか。そういう研究もありそうではある。

ゼロ

個人的にはゼロはビットレベルでも00000000であった方が簡単そうな気がする。そして実際に、浮動小数点数のゼロは00000000である。正確には、指数部と仮数部が両方ゼロである場合、値はゼロとなる。しかし、浮動小数点数が符号ビットを持っている都合上ゼロにも符号があり、+0と-0が存在している。演算の際に特に違いはない。

これは先に述べた「指数部が0b0000'0000の際の特殊な値」のうちの一つである。感覚的にも、指数が小さくなるとゼロに近づいていくわけで、指数部が最小の値になると突然ゼロになるというのも、そこまでの飛躍には感じないのではなかろうか。

非正規化数

さて、ゼロが「指数部と仮数部が両方ゼロである場合」なら、指数部がゼロで仮数部が非ゼロだった場合はどんな値になるのか。それが非正規化数である。これは先に述べた「指数部が0b0000'0000の際の特殊な値」のもう一つのパターンとなる。

非正規化数の指数部はゼロであるため、絶対値が小さい側にあるのだろうと予想できる。そして実際に非正規化数は絶対値が小さい。これがどこに位置しているかというと、最小の正規化数からゼロまでの間である。最小の正規化数は単精度浮動小数点数においては1.000x2^-126である。指数部がゼロでない最小の値、つまり1のとき、バイアスを考慮するとその指数は-126になるためだ。非正規化数を考慮しなければ、この数の次に絶対値が小さい値は0になる。0 ~ 1 x2^-126の範囲は表現されない。同じくらい細かい、1 ~ 2 x2^-126の範囲は23bitもの精度で表現されるにもかかわらず。

この範囲を正規化数で埋めようとしても、右半分（[2^(-127), 2^(-126))）しか埋まらないのは簡単にわかる。そこで、この範囲を1~2 x2^-126と同じ幅で分割してしまうというのが非正規化数である。その表現範囲は[0, 1x2^-126)となる。よって非正規化数の1の位はゼロとなり、その名の通り正規化されていない数となる。正規化数とは、最初の意味のある桁が1の位であり、かつ1の位が非ゼロなものを指すのであった。なので非正規化数ではケチ表現での暗黙の1は存在せず、1桁目には暗黙の0が存在する。

図3. 最小の正規化数（exponent = 1の部分）と非正規化数（青色）が表現する範囲。非正規化数は最小の正規化数からゼロまでを、最小の正規化数と同じ精度（`f32`なら2^-126）で表現する。全てを正規化数とした場合（上段）、赤色斜線の範囲`[0, 2^(-127))`が表現できない。

ところで、この表現での最小の数は0であり、その表現は0.0000x2^-126なので、指数部と仮数部がともにゼロとなる。これは先に述べたゼロの表現と一致している。このようにすることで、最後の正規化数からゼロまでが綺麗に繋がる。

非数と無限

浮動小数点数演算の結果として、浮動小数点数の範囲内では表現できないような値が出現することがあり得る。そのような数を表現するために、浮動小数点数には非数（NaN）と無限大（Inf）が存在する。これらが、「指数部が0b1111'1111の際の特殊な値」である。NaNは置いておくとして、無限大を導入することを認めてそれをどう符号化するかを考えれば、指数部が大きくなると値は指数的に大きくなるわけで、指数が最大値になると無限大になるというのがちょうどいい場所だろう。

NaNとInfは、指数部のビットがすべて1、つまり指数部が最大の値を取る。そのうえで、仮数部がゼロであればInf、そうでなければ（一つでも1であるビットがあれば）NaNとなる。よってNaNは仮数部だけで2²³-1（倍精度なら2⁵²-1）通りの異なる値を取ることができる。余談だが、言語処理系などの実装では、この隙間に小さな整数を埋め込むというテクニックが存在する（NaN boxing）²。また、符号ビットに関しては制約がないので、InfとNaNにも正負がある。NaNはともかくとして、Infの正負には演算においても意味がある。

これらは特定の演算の結果として出てくる。例えば、演算の結果が浮動小数点数の範囲では表現しきれない大きな値になったときは、通常はInfが帰ってくることになる。非数は、0/0 や inf - inf 、そして複素数への変換が暗黙に行われない場合のsqrt(-1)などの結果として発生する。

InfやNaNなどの特殊な数は、演算においても特別扱いされるため、実装する際には念頭に置いておく必要がある。これらは演算を実装する際に必要に応じて説明する。

丸め

浮動小数点数の桁数が有限である以上、計算結果がその範囲を超えた際には、下の桁を忘れざるを得ない。そのような場合に下の桁をどう扱うかが、丸めモードで規定されている。

通常は「最近接（偶数）丸め」が採用されており、今回の記事もこれだけを考慮する。最も使われており、かつ最もややこしい丸めモードであるように思う。これは基本的には最近接の値に丸めるという方針だが、ちょうど真ん中（二進数なので0.101は0.10と0.11のちょうど真ん中にある）の場合には、上の桁が偶数になるように丸めるというモードだ（先の例の場合、0.10にする）。この丸めモードでは、切り上げるか切り下げるかを決定するのに、「今から落とすので丸めたい桁」「丸めたい桁より下がすべてゼロかどうか（丸めたい桁は前後の数のちょうど真ん中かどうか）」「丸めたい桁の一つ上の桁は偶数かどうか」の全てを知っていなければならない。

ほかのモードには、最近接（0から離れる）丸め、切り上げ、切り下げ、切り捨てなどがある。が、今回は深入りしない。基本的には、上記の情報に加えて符号ビットを知っていれば問題なく実装できるはずだ。

おわりに

浮動小数点数の性質についてのおさらいはもうこれで十分だろう。これだけわかっていれば今後演算を考える際に困ることはない。次回は実際に浮動小数点数の加算を考えてみる。

より細かくIEEE仕様について知りたい人には、技術書典で販売されていた『浮動小数点数小話』（だめぽラボ）が日本語かつよくまとまっており、参考になる。

一応注意しておくと、この記事の内容は特に浮動小数点数の策定の歴史などについて調べたものではなく、私が勝手に解釈したものなので、この形が選ばれた実際の理由とは異なる可能性がある。↩
例として、動的型付け言語の処理系を書いているとしよう。変数を保持する型は基本的にはオブジェクトへのポインタにしておけばよいのだが、浮動小数点数や32bit整数くらいの小さなプリミティブ型ならポインタを経由させずそのまま持っていた方が効率が良い（しかも、プログラム内で出てくる大抵の整数は32bitの範囲よりも十分小さく、余裕をもって格納できる）。というわけで、変数の内部表現を浮動小数点数にしておいて、NaNの場合は浮動小数点数以外の値である、ということにする。そしてNaNの使われていない仮数部を32bit整数やシンボルID、オブジェクトへのポインタを格納するために使うということだ。いや32bit整数が64bit浮動小数点数の仮数部（52bit）に入るのはわかるが、ポインタは無理だろう？　と思われるかもしれないが、実際にはx86_64ではアドレスは実質的には48bitしか使われておらず（『低レベルプログラミング』などを参照）、ギリギリ入るのである。↩

2021-08-31

boost-ext/ut の使い方

C++

しばらくブログを書けていなかったのでちょっと準備運動をする。比較的長めのものをこれから書こうと思っているからだ。

github.com

boost-ext/μtは、C++20用のテストライブラリだ。C++20らしくモジュールとしても使えるし、シングルヘッダオンリーライブラリとしても使える。

うれしいことにこれはCatch2と比べて非常にコンパイルが速く、Boost.UnitTestFrameworkと比べて非常に軽量だ。

https://github.com/boost-ext/ut#benchmarks

テストコードはラムダを使って書く。

#include <concepts>
#include <iostream>
#include <boost/ut.hpp>

template<std::unsigned_integral UInt>
constexpr UInt factorial(UInt x)
{
    return (x == 0) ? 1 : x * factorial(x-1);
}

int main()
{
    using namespace boost::ut::literals; // to use operator ""_test
    "factorial"_test = []
    {
        boost::ut::expect(factorial(0u) == 1u);
        boost::ut::expect(factorial(1u) == 1u);
        boost::ut::expect(factorial(2u) == 2u);
        boost::ut::expect(factorial(3u) == 6u);
        boost::ut::expect(factorial(4u) == 24u);
    };
    return 0;
}

この""_testは好きなところに書けるので、（コードと同じファイルにテストを書きたい、などの理由で）テストのためだけに.cppを用意したくない場合、headerであろうと書くことができる。そう、inline変数がC++20には（C++17から）あるのだ。

// factorial.hpp
namespace lib
{
template<std::unsigned_integral UInt>
constexpr UInt factorial(UInt x)
{
    return (x == 0) ? 1 : x * factorial(x-1);
}
} // lib

#ifdef ACTIVATE_UNIT_TEST
#include <boost/ut.hpp>

inline boost::ut::suite test_factorial = []
{
    using namespace boost::ut::literals; // to use ""_test
    "factorial"_test = []
    {
        boost::ut::expect(lib::factorial(0u) == 1u);
        boost::ut::expect(lib::factorial(1u) == 1u);
        boost::ut::expect(lib::factorial(2u) == 2u);
        boost::ut::expect(lib::factorial(3u) == 6u);
        boost::ut::expect(lib::factorial(4u) == 24u);
    };
};
#endif

こうしておけばmain.cppからincludeされているものはすべて、ACTIVATE_UNIT_TESTを定義している限り、テストが実行される。いやまあ、明らかにスケールしないのでファイルを分けてfactorial_test.cppみたいなものの中に書くべきだが、数ファイル以下の簡単なプロジェクトならこの程度から始めてもいいのではないか。気軽に行きましょう。

テストを有効化する際にマクロを使っているのは、せっかくmacro-freeなライブラリを使っているのに……という気持ちになるし、別にfactorial_test.cppみたいなやつ用意すればいいじゃないとも思うが、まあ。

ログを取りたいときはboost::ut::logを使う。streamっぽいインターフェースで、改行が自動的に行われる。

boost::ut::suite test_factorial = []
{
    using namespace boost::ut::literals; // to use ""_test
    "factorial"_test = []
    {
        boost::ut::log << "testing factorial() function ...";
        boost::ut::expect(lib::factorial(0u) == 1u);
        boost::ut::expect(lib::factorial(1u) == 1u);
        boost::ut::expect(lib::factorial(2u) == 2u);
        boost::ut::expect(lib::factorial(3u) == 6u);
        boost::ut::expect(lib::factorial(4u) == 24u);
    };
};

テストが落ちたときに出力する内容は、expect自体に流し込むとよい。こちらも

boost::ut::suite test_factorial = []
{
    using namespace boost::ut::literals; // to use ""_test
    "factorial"_test = []
    {
        boost::ut::log << "testing factorial() function ...";
        boost::ut::expect(lib::factorial(0u) == 1u) << "expecting 1 but got " << lib::factorial(0u);
        boost::ut::expect(lib::factorial(1u) == 1u) << "expecting 1 but got " << lib::factorial(1u);
        boost::ut::expect(lib::factorial(2u) == 2u) << "expecting 2 but got " << lib::factorial(2u);
        boost::ut::expect(lib::factorial(3u) == 6u) << "expecting 6 but got " << lib::factorial(3u);
        boost::ut::expect(lib::factorial(4u) == 24u) << "expecting 24 but got " << lib::factorial(4u);
    };
};

boost-extはほかにも様々な機能を持っているが、最低限これだけで使えないことはない。

ビルドが速いので、趣味でC++20を使えるプロジェクトでパパっとテストを書きたいときはかなりよい選択肢ではないだろうか。

boost-extはboost本体の一部ではないが、ほかにもいくつかライブラリを持っている。ちょっと見てみると面白いのではないか。

2021-06-06

Boost math constantsの変遷記録

C++

今日気づいたのだが、Boost.math.constants にある one_div_pi は Boost 1.71.0 以前には存在しない。

背景

Boost.math.constantsは、現時点ではC++で数学定数を取得するために最もよい方法だろう。これは、以下のようにして数学定数を取得できるライブラリだ。円周率以外にも、たいていのよく使う定数はすでに入っている。

一応、少しコードを書くことで定数を追加したり、普通ではない実数型（任意精度実数型とか）に対応することも可能なようだ。

#include <boost/math/constants/constants.hpp>
constexpr auto pi = boost::math::constants::pi<double>();

www.boost.org

これに対して、非常によく使用されているが実は仕様外である、M_PIなどのマクロ定数がある。非常に厳密に言うならば、処理系はこのようなマクロを定義してはいけない。まあこのブログを読みに来た人にはどこかで聞いたことがある話だと思う。

qnighy.hatenablog.com

ほかに、将来的によりよくなるはずの方法として、C++20の<numbers>ヘッダがある。Boostと比べると定義してある定数の種類は少ないが、これでも実用上困ることはないだろう。また、標準ライブラリなので基本的に依存関係を心配せずに使えるというメリットもある。とはいえ、C++20を使えるプロジェクトはまだそう多くはないだろうから、もうしばらくの間はBoostの方が使う機会が多いのではないか。

cpprefjp.github.io

Boost.constantsの変遷

さて、今日は別のマシンで書いていたコードを家のマシンにcloneしていじろうとしたところ、boost::math::constants::one_div_piがないというエラーが出て、焦っていた。どうやらBoost 1.71.0にはこれがないらしい。リファレンスを見たところ、Boost 1.72.0で追加されたもののようだ。一応Boostのchangelogを見に行ったが、Boost全体のchangelogともなるとそれぞれがここまで些細なことを報告していると終わらなくなるのか、記載がない。

www.boost.org

そこでBoost.mathのレポジトリを見に行ってみたが、個別のリリースノートのようなものは書いていないようだ。一番最近のものには少し書かれているが、古いものにはあまりない。

github.com

Boost.mathのドキュメントのリリースノートにもそれらしい記載はなかった。

www.boost.org

これでは気づけないのも当然という気がする。とはいえこれでは少し困るので、ちょっと変遷を追いかけてみた。

BoostのWebサイトはURLにバージョンが入っているので、適当なシェルスクリプトでバージョンを回しながらwgetしてdiffを取ると簡単に変更履歴を作れる。どこまで遡るかは少し迷ったが、Ubuntu18.04のaptで入るのが1.65.0っぽいので、それより古いのはもう見なくてよかろうということで65以降を見ることにする。

1.65.0 -> 1.71.0

この間、math.constantsには特に変化はなかった。バージョン番号が粛々と上がり、Contributorの数が少し増えていた。

1.71.0 -> 1.72.0

ここでそこそこの量の定数が追加されている。

等価なPOSIXのマクロ（M_PIみたいなやつ）の記述がドキュメントに足された
quarter_pi が追加された。
one_div_pi が追加された。
two_div_pi が追加された。
two_div_root_pi が追加された。
log2_e が追加された。

1.72.0 -> 1.73.0

ドキュメントのリファクタリングが行われている。

1.73.0 -> 1.74.0

変化なし。

1.74.0 -> 1.75.0

そんな頻繁に使うか？　というような定数がたくさん導入されている。一部には予想される使用頻度に比べて圧倒的に一般的な名前がつけられているような気がしなくもない……。

first_feigenbaum が追加された（マジか？）ファイゲンバウム定数 - Wikipedia
plastic が追加された。プラスチック数 - Wikipedia
gauss が追加された。Gauss's constant - Wikipedia
dottieが追加された。Dottie number - Wikipedia
reciprocal_fibonacciが追加された。フィボナッチ数列の逆数和 - Wikipedia
laplace_limitが追加された。Laplace limit - Wikipedia

1.75.0 -> 1.76.0

特に変化はない。

おわり

one_div_piみたいな頻出っぽいものが1.72.0まで入ってないというのは少し驚いた。でもよく思い返してみると数年前には「なんでone_div_piがないんだよ（ﾌﾞﾁｷﾞﾚ）」みたいに言いながら自分で定数書いてた記憶があるな。

こういう明らかに頻出なものが割と最近まで入ってなかったかと思えば、これそんな頻繁に使うか？　みたいな値がしれっと入ってたりもするので、結構意外な部分が大きい。どのへんまでをユーザーにやらせて、どこからはライブラリが責任もってメンテするかを決めるのは大変そうですね（他人事）。

2021-06-05

UARTで送受信

FPGA

昨日の夜、"Hello World"を送信する回路がちゃんと動いて、安心して寝た。今日はPC -> FPGAの受信を書き、とりあえずこちらが送った文字をそのまま返すだけの回路を作った。少しは慣れてきたのか、シミュレーションでデバッグしたあと実機に焼いたら即動いたのでガッツポーズしてしまった。というのも、数日前まではシミュレーションで動くように見えてもビットストリームを作れないような回路とか、実機では動かないような回路を書いてしまっていたので……。

今日、途中でシミュレーションしようとしても「executing analysis and compilation step」のダイアログが出たまま始まらなくなってしまい、何かおかしくなったのかとシミュレータを閉じたり、Vivadoを閉じたり、Windowsを再起動しても直らなかったのでほげ～と言いながらググっていたら以下のような回答が出てきた。

forums.xilinx.com

これにある通り、tclコンソールにreset_simulation -simset sim_1 -mode behavioralと入力すると動くようになった。何だったんだ。

しばらくちゃんと本を読んだり他人のコードを読んだりしていて、今まで（といっても今日で書き始めて1週間なのだが）regを意味もなく多用していたことに気づいた。その瞬間の入力の組み合わせだけで問題ない部分はwireでよい。ていうかなんでregばっかり使ってたんだろうな。

ところで、wireに対してifを使おうとしたときfunctionまみれになるのはどうしたらいいんだろう。functionで一つの変数しか返していないので無駄に分割された大量のコードが並ぶようになってしまった。もちろん、functionの返り値をassign {val1, val2} = next_value(...)のようにしてパック展開（？）で受ければよいのだが、これはこれでまた若干面倒くさい。何かいい書き方があるのを知らないだけな気がするのだけど。SystemVerilogではalways_combが使えるのだが。

次にすることを考える。とりあえず文字列を送受信できるようになったので、何かしらの簡単な計算をする回路を作れるはずだ。例えばmd5sumとかはできるだろう。とはいえ一足飛びにそこまで行くのは大変そうなので、まずは単に文字列を覚えてあとで返すようなものを作った方がよさそう。ヴィジュネル暗号とかだと少し楽しいだろうか？　もう少し先の話としては、Brainfuckのインタプリタなどは楽しそうだしやってみたいと思っていた。

その前に少しリファクタリングと機能追加をした方がいいかもしれない。例えば、送受信回路にバッファ用のメモリを一枚噛ませることで、処理を中断させずに送信用のデータをためたり、読み込みが終わっているかどうか心配せずに受信データを更新したりできるようにしておきたい。まあそのメモリが溢れたら止めざるを得ないが、ないよりましだろう。特に今は受信データは次のデータが来た瞬間に問答無用で消えてしまうので、かなりタイミングがシビアになっている。これはよくない。

ここまでとりあえずVerilogから勉強していくか、と思ってVerilogの本を読んでいたが、普通にSystemVerilogの文法のさわりだけでも知っているとパク……参考にできるコードの幅が広がるので両方やったほうがよさそう。最終的にChiselまで触る気ではいる（これはRustを勉強する前にC++を勉強する前にCを勉強するようなもの（メリットもあるがコストも高い）なのではないかという気はしたものの、性格的にはその方が自分には合っているのではないかという気がしている。それだけのコストをかけるだけの余裕があるかというのは年々怪しくなっているが……）。

Vivadoで使えるテキストエディタにGVimがあったのでGVimを導入して.vimrcなどを設定したが、vivadoが出してくれるエラーが表示できない。そういうプラグインがあるだろうと思ったが、すぐには見つからなかった。あとで気合を入れて探してみるか。

そうそう、それからコーディングスタイルをとっとと固めておいた方がいいな。どういう風に書くのが普通なのかあまりよく知らないので今はなんか適当に書いてる。

 module top(CLK100MHZ, BUTTON, uart_rxd_out, uart_txd_in, led0, led1);
     input  wire      CLK100MHZ;
     input  wire      BUTTON;
     input  wire      uart_txd_in;
     output wire      uart_rxd_out;
     output wire[2:0] led0;
     output wire[2:0] led1;
 
     wire      uart_send_enable;
     wire[7:0] uart_send_data;
     wire      uart_sending;
 
     uart_send send(
         .clock(CLK100MHZ),
         .reset(BUTTON),
         .uart_enable(uart_send_enable),
         .uart_data(uart_send_data),
         .uart_busy(uart_sending),
         .uart_tx(uart_rxd_out),
         .led(led0)
         );
 
     assign led1 = 3'b000;
     wire[7:0] uart_recv_data;
     wire      uart_receiving;
     wire      uart_recv_okay;
 
     uart_recv recv(
         .clock(CLK100MHZ),
         .reset(BUTTON),
         .uart_data(uart_recv_data),
         .uart_busy(uart_receiving),
         .uart_okay(uart_recv_okay),
         .uart_rx(uart_txd_in),
         .led(led1)
         );

    reg[7:0] data;
    reg data_sent;
    wire has_data = (~uart_receiving) && uart_recv_okay;

    assign uart_send_data = data;

    parameter IDLE_STATE = 0;
    parameter SEND_STATE = 1;
    parameter WAIT_STATE = 2;
    reg [1:0]   state = IDLE_STATE;
    wire[1:0] w_state;

    assign uart_send_enable = state == SEND_STATE;

    function [1:0] next_state(
        input[1:0] state,
        input      uart_sending,
        input      has_data,
        input      data_sent
        );
        if (state == IDLE_STATE) begin
            if (has_data && (~data_sent)) begin
                if (uart_sending) begin
                    next_state = WAIT_STATE;
                end else begin
                    next_state = SEND_STATE;
                end
            end else begin
                next_state = IDLE_STATE;
            end
        end else if (state == WAIT_STATE) begin
            if (uart_sending) begin
                next_state = WAIT_STATE;
            end else begin
                next_state = SEND_STATE;
            end
        end else begin // SEND_STATE
            next_state = IDLE_STATE;
        end
    endfunction
    assign w_state = next_state(state, uart_sending, has_data, data_sent);
    
    always @(posedge CLK100MHZ) begin
        if (BUTTON) begin
            state     <= IDLE_STATE;
            data      <= 8'b0;
            data_sent <= 1'b0;
        end else begin
            state <= w_state;
            
            if (uart_recv_okay) begin
                data <= uart_recv_data;
            end else begin
                data <= 8'b0;
            end
            
            if (uart_receiving) begin
                data_sent <= 1'b0;
            end else if (state == SEND_STATE) begin
                data_sent <= 1'b1;
            end
        end
    end
 endmodule

 module uart_send(clock, reset, uart_enable, uart_data, uart_busy, uart_tx, led);
     input  wire       clock;
     input  wire       reset;
     input  wire       uart_enable;
     input  wire [7:0] uart_data;
 
     output wire       uart_busy;
     output wire       uart_tx;
     output wire [2:0] led;
 
     parameter CLK_PER_BIT = 868; // 100 MHz / 115200 Hz
 
     parameter IDLE_STATE = 0;
     parameter SEND_STATE = 1;
 
     reg  state = IDLE_STATE;
     wire w_state;
 
     reg [9:0] data = 10'b1111111111;
     wire[9:0] w_data;
 
     reg [9:0] clock_counter = 10'b0;
     wire[9:0] w_clock_counter;
 
     reg [3:0] bit_counter = 4'b0;
     wire[3:0] w_bit_counter;
 
     assign uart_tx   = data[0];
     assign uart_busy = (state == IDLE_STATE) ? 1'b0 : 1'b1;
 
     assign led[2:0]  = (state == IDLE_STATE) ? 3'b001 : 3'b010;
 
     // ----------------------------------------------------------------------
     // update state
 
     function [0:0] next_state(
         input      state,
         input      enable,
         input[9:0] clock_counter,
         input[3:0] bit_counter
         );
 
         if (state == IDLE_STATE) begin
             if(enable) begin
                 next_state = SEND_STATE;
             end else begin
                 next_state = IDLE_STATE;
             end
         end else begin // SEND_STATE
             if (clock_counter == CLK_PER_BIT-1) begin
                 if (bit_counter == 4'd9) begin
                     next_state = IDLE_STATE;
                 end else begin
                     next_state = SEND_STATE;
                 end
             end else begin
                next_state = SEND_STATE;
             end
         end
     endfunction
 
     assign w_state = next_state(state, uart_enable, clock_counter, bit_counter);
 
     // ----------------------------------------------------------------------
     // update clock counter
 
     function [9:0] next_clock_counter(
         input      state,
         input[9:0] clock_counter
         );
 
         if (state == IDLE_STATE) begin
             next_clock_counter = 10'b0;
         end else begin
             if (clock_counter == CLK_PER_BIT-1) begin
                 next_clock_counter = 10'b0;
             end else begin
                 next_clock_counter = clock_counter + 1;
             end
         end
     endfunction
 
     assign w_clock_counter = next_clock_counter(state, clock_counter);
 
     // ----------------------------------------------------------------------
     // update number of bits sent
 
     function [3:0] next_bit_counter(
         input      state,
         input[9:0] clock_counter,
         input[3:0] bit_counter
         );
 
         if(state == IDLE_STATE) begin
             next_bit_counter = 4'b0;
         end else begin
             if (clock_counter == CLK_PER_BIT-1) begin
                 if (bit_counter == 4'd9) begin
                     next_bit_counter = 4'd0;
                 end else begin
                     next_bit_counter = bit_counter + 1;
                 end
             end else begin
                 next_bit_counter = bit_counter;
             end
         end
     endfunction
 
     assign w_bit_counter = next_bit_counter(state, clock_counter, bit_counter);
 
     // ----------------------------------------------------------------------
     // update data to send
 
     function [9:0] next_data(
         input      state,
         input      enable,
         input[7:0] uart_data,
         input[9:0] data,
         input[9:0] clock_counter
         );
 
         if (state == IDLE_STATE) begin
             if (enable) begin
                 next_data = {1'b1, uart_data, 1'b0};
             end else begin
                 next_data = data;
             end
         end else begin
             if (clock_counter == CLK_PER_BIT - 1) begin
                 next_data = {1'b1, data[9:1]};
             end else begin
                 next_data = data;
             end
         end
     endfunction
     assign w_data = next_data(state, uart_enable, uart_data, data, clock_counter);
 
     // ----------------------------------------------------------------------
     // update registers
 
     always @(posedge clock) begin
         if (reset) begin
             state         <= IDLE_STATE;
             clock_counter <= 10'b0;
             bit_counter   <=  4'b0;
             data          <= 10'b1111111111;
         end else begin
             state         <= w_state;
             clock_counter <= w_clock_counter;
             bit_counter   <= w_bit_counter;
             data          <= w_data;
         end
     end
 endmodule

module uart_recv(clock, reset, uart_data, uart_busy, uart_okay, uart_rx, led);
    input  wire       clock;
    input  wire       reset;
    output wire [7:0] uart_data;

    output wire       uart_busy;
    output wire       uart_okay;
    input  wire       uart_rx;
    output wire [2:0] led;

    parameter CLK_PER_BIT = 868; // 100 MHz / 115200 Hz

    parameter IDLE_STATE = 0;
    parameter CHCK_STATE = 1; // checking start bit
    parameter RECV_STATE = 2;
    parameter STOP_STATE = 3; // receiving stop bit

    reg [1:0] state = IDLE_STATE;
    wire[1:0] w_state;

    reg [9:0] clock_counter = 10'b0;
    wire[9:0] w_clock_counter;

    reg [3:0] bit_counter = 4'b0;
    wire[3:0] w_bit_counter;

    reg [9:0] data = 10'b1111111111;
    wire[9:0] w_data;

    assign uart_data = data[8:1]; // except start/stop bits
    assign uart_okay = (data[0:0] == 1'b0) && (data[9:9] == 1'b1); // start with 0, end with 1
    assign uart_busy = (state == RECV_STATE) ? 1'b1 : 1'b0;
    assign led[2:0]  = (state == IDLE_STATE) ? 3'b001 :
                       (state == CHCK_STATE) ? 3'b010 :
                       (state == RECV_STATE) ? 3'b100 : 3'b111;

    // ----------------------------------------------------------------------
    // update state

    wire rx_is_zero;
    assign rx_is_zero = (uart_rx == 1'b0);

    function [1:0] next_state(
        input[1:0] state,
        input      uart_rx,
        input      rx_is_zero,
        input[9:0] clock_counter,
        input[3:0] bit_counter
        );

        if (state == IDLE_STATE) begin
            if(rx_is_zero) begin
                next_state = CHCK_STATE;
            end else begin
                next_state = IDLE_STATE;
            end
        end else if (state == CHCK_STATE) begin
            if (clock_counter == (CLK_PER_BIT / 2) - 1) begin
                if (rx_is_zero) begin
                    next_state = RECV_STATE;
                end else begin
                    next_state = IDLE_STATE;
                end
            end else begin
                next_state = CHCK_STATE;
            end
        end else if (state == RECV_STATE) begin
            if (clock_counter == CLK_PER_BIT-1) begin
                if (bit_counter == 4'd8) begin
                    next_state = STOP_STATE;
                end else begin
                    next_state = RECV_STATE;
                end
            end else begin
               next_state = RECV_STATE;
            end
        end else begin // STOP_STATE
            if (clock_counter == (CLK_PER_BIT / 2) - 1) begin
                next_state = IDLE_STATE;
            end else begin
                next_state = STOP_STATE;
            end
        end
    endfunction

    assign w_state = next_state(state, uart_rx, rx_is_zero, clock_counter, bit_counter);

    // ----------------------------------------------------------------------
    // update clock counter

    function [9:0] next_clock_counter(
        input[1:0] state,
        input[9:0] clock_counter
        );

        if (state == IDLE_STATE) begin
            next_clock_counter = 10'b0;
        end else if(state == CHCK_STATE) begin
            if (clock_counter == CLK_PER_BIT / 2 - 1) begin
                next_clock_counter = 10'b0;
            end else begin
                next_clock_counter = clock_counter + 1;
            end
        end else begin
            if (clock_counter == CLK_PER_BIT-1) begin
                next_clock_counter = 10'b0;
            end else begin
                next_clock_counter = clock_counter + 1;
            end
        end
    endfunction

    assign w_clock_counter = next_clock_counter(state, clock_counter);

    // ----------------------------------------------------------------------
    // update number of bits sent

    function [3:0] next_bit_counter(
        input[1:0] state,
        input[9:0] clock_counter,
        input[3:0] bit_counter
        );

        if(state == IDLE_STATE) begin
            next_bit_counter = 4'b0;
        end else if(state == CHCK_STATE) begin
            next_bit_counter = 4'b0;
        end else begin
            if (clock_counter == CLK_PER_BIT-1) begin
                if (bit_counter == 4'd9) begin
                    next_bit_counter = 4'd0;
                end else begin
                    next_bit_counter = bit_counter + 1;
                end
            end else begin
                next_bit_counter = bit_counter;
            end
        end
    endfunction

    assign w_bit_counter = next_bit_counter(state, clock_counter, bit_counter);

    // ----------------------------------------------------------------------
    // update received data

    function [9:0] next_data(
        input[1:0] state,
        input      uart_rx,
        input[9:0] data,
        input[9:0] clock_counter
        );

        if (state == IDLE_STATE) begin
            next_data = data;
        end else if (state == CHCK_STATE) begin
            if (uart_rx == 1'b0) begin
                next_data = 10'b0111111111;
            end else begin
                next_data = data;
            end
        end else if (state == RECV_STATE) begin
            if (clock_counter == CLK_PER_BIT - 1) begin
                next_data = {uart_rx, data[9:1]};
            end else begin
                next_data = data;
            end
        end else begin
            next_data = data;
        end
    endfunction
    assign w_data = next_data(state, uart_rx, data, clock_counter);

    // ----------------------------------------------------------------------
    // update registers

    always @(posedge clock) begin
        if (reset) begin
            state         <= IDLE_STATE;
            clock_counter <= 10'b0;
            bit_counter   <=  4'b0;
            data          <= 10'b1111111111;
        end else begin
            state         <= w_state;
            clock_counter <= w_clock_counter;
            bit_counter   <= w_bit_counter;
            data          <= w_data;
        end
    end
endmodule

はじめに

constexprの発展史

C++11

constexpr変数

constexpr関数

C++14

制限緩和

<array>, <chrono>, <complex>, <initializer_list>, <tuple>, <utility>の一部

C++17

constexpr lambda

if constexpr

ライブラリ対応

C++20

継承

動的メモリ確保（new/delete、std::vectorとstd::string）

共用体

文法上の制限緩和

consteval

is_constant_evaluated

<algorithm>と<numeric>、それに関係したライブラリ機能

<complex>

C++23

if consteval

文法上の制限緩和

簡単な数学関数

C++26

数学関数

型消去

<algorithm>で前回スルーされていたもののいくつか

TMP

C++23でのコンパイル時レイトレーシング

画像ファイル出力

数学関数

乱数

オブジェクトのマテリアル

実行

実際のコード

おわりに

やり方

これだと全員に適用されるだろ

なんで最初に<Space>をunmapしてるの？

最後の長いの何？

個人用メモにgrowiってオーバースペックじゃない？

std::source_locationとは

問題

解決方法

限定付きのよりよい解決策

現実の浮動小数点数

浮動小数点数の基本的構造

なぜ1から2の範囲なのか

ゼロ

非正規化数

非数と無限

丸め

おわりに

背景

Boost.constantsの変遷

1.65.0 -> 1.71.0

1.71.0 -> 1.72.0

1.72.0 -> 1.73.0

1.73.0 -> 1.74.0

1.74.0 -> 1.75.0

1.75.0 -> 1.76.0

おわり

`constexpr`変数

`constexpr`関数

`<array>`, `<chrono>`, `<complex>`, `<initializer_list>`, `<tuple>`, `<utility>`の一部

`constexpr lambda`

`if constexpr`

動的メモリ確保（`new/delete`、`std::vector`と`std::string`）

`consteval`

`is_constant_evaluated`

`<algorithm>`と`<numeric>`、それに関係したライブラリ機能

`<complex>`

`if consteval`

`<algorithm>`で前回スルーされていたもののいくつか

なんで最初に`<Space>`を`unmap`してるの？

`std::source_location`とは